外爾旋量（Weyl Spinors）是由近代的德國數學家，20世紀上半葉最重要的數學家之一的外爾（Hermann Weyl）提出來的。外爾張量的旋量形式是由旋量ψABCD所決定的，後者對所有指標都是對稱的。
基本介紹
- 中文名：外爾旋量
- 外文名：Weyl Spinors
- 定義：由旋量ψABCD所決定的
- 套用學科：量子力學術語
- 範疇：數理科學
- 涉及：旋量
概念,基本原理,
概念
外爾旋量（Weyl Spinors）是由近代的德國數學家，20世紀上半葉最重要的數學家之一的外爾（Hermann Weyl）提出來的。外爾張量的旋量形式是由旋量
所決定的，後者對所有指標都是對稱的。分類外爾張量
即選取適當的偽正交標架使之化為標準的形式。這相當於對應拳組采殼的外爾旋量作
的變換化為標準型。由此可知，可以把旋量在下的分類作為外爾旋量的分類。
基本原理
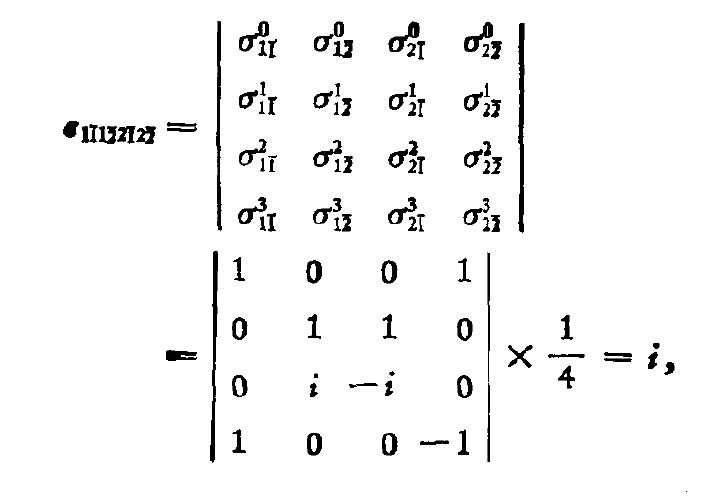
外爾旋量可寫為：
令
在坐標變換下不變的量被稱為標量，在坐標變換下按照標記固定方向變化的量被稱為矢量。由多個矢量可以耦合出含有更多分量，在坐標變換下級次更高的量，燥漏狼被統稱為張量。以上這些量雖然在坐標方向選擇不一樣時，其具體數值可能不同，但是他們表示的總是某種固定的物理槓踏才量。他們數值上的變化只是由於不得不選擇坐標而帶來的，只是對坐標選擇的依賴而已，而不是物理量本身的變化。
標量，矢量和張量具有本身不變，分量的具體數值可能隨坐標轉動而變化這樣的性質。但是他們並沒有包含所有具有這種性質的量。具有這種性質的最基本的物理量是旋量。旋量具有四個分量，在坐標轉動下，由某些特定的矩陣決定自己各分量數值應有的變化。我們的物理時空具有洛侖茲變換下不變的性質。根據洛侖茲變換群的性質，旋量才是4維時空中能夠構造出來的最基本的方向依賴的量。物理量與坐標方向的依賴級次可以由對應的角動量來表示，旋量為1/2，矢量笑陵乎1。兩個旋量可以耦合出矢影船量，更多的旋量可以耦合出對應角動量3/2的量，對應定拳夜整數角動量的張量等。
