基本介紹
- 中文名:夏普爾定理
- 外文名:Chapple theorem
- 所屬學科:數學
- 所屬問題:平面幾何(三角形)
- 別稱:(三角形的)歐拉定理
定理及簡史,定理的證明,夏普爾定理的逆命題,定理的引申與推廣,定理的引申,定理的推廣,
定理及簡史
設⊙O1、⊙O2的半徑分別為r和R,圓心距為d,若存在一個三角形以⊙O1為內切圓(或旁切圓),同時又內接於圓⊙O2,則
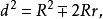
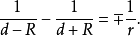
上述定理被稱夏普爾定理(Chapple theorem)或稱為關於三角形的歐拉定理,但不論屬於誰,這一定理的發現至今已有二百多年的歷史,而且歐拉的學生富斯(N.Fuss,1755 ~ 1825)在1798年還給出了它的一個推廣。
定理的證明
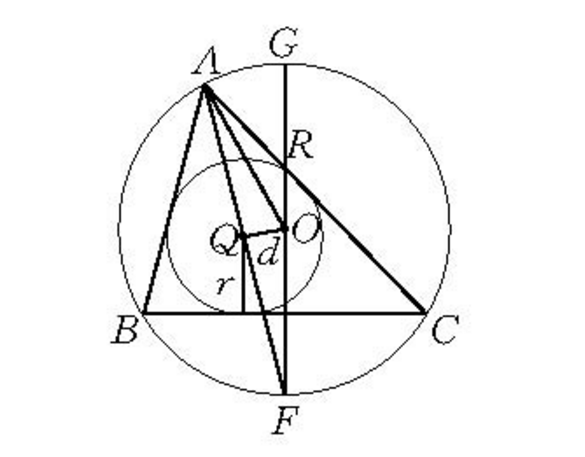
證明 如圖1(a),聯結AO1,設其所在直線交⊙O2於D,聯結BD,再過O1作⊙O2的直徑EF,則由圓冪定理有
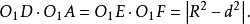
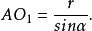
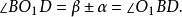
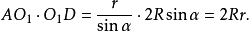
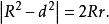
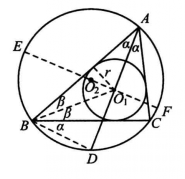 圖1(a)
圖1(a) 圖1(b)
圖1(b)夏普爾定理的逆命題
夏普爾定理的逆命題也成立。
逆定理 設⊙O1、⊙O2的半徑分別為r和R,圓心距為d,若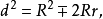 則存在一個△ABC,它外切(或旁切)於⊙O1,又內接於⊙O2。
則存在一個△ABC,它外切(或旁切)於⊙O1,又內接於⊙O2。
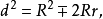
證明 如圖2(a),在⊙O2上任取一點A,聯結AO1交⊙O2於D,在⊙O2上取點B、C,使DB = DC = DO1。
因為
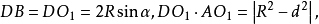
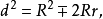
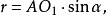

又因為∠DBO1= ∠BO1D=β±α,
∠DBC=∠DAC=α,
所以 ∠O1BC=(β±α)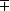 α=β。
α=β。
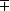
證畢。
定理的引申與推廣
定理的引申
在歐拉定理中,若⊙O1為△ABC內切圓時,因為d2=R2-2Rr≥0,所以R≥2r,從而有
定理1 若△ABC外接圓半徑為R,內切圓半徑為r,則R≥2r。
定理的推廣
將三角形推廣到四邊形,得到
定理2 設⊙O1、⊙O2的半徑分別為r、R,圓心距為d,若存在一個四邊形ABCD外切於⊙O1且內接於⊙O2,則
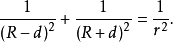
定理3若凸四邊形既有外接圓又有內切圓,且外接圓半徑為R,內切圓半徑為r,則
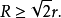
更一般地,還有
定理4若凸n邊形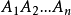 既有外接圓又有內切圓,設其外接圓半徑為R,內切圓半徑為r,則
既有外接圓又有內切圓,設其外接圓半徑為R,內切圓半徑為r,則
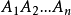
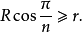
證明略。