基本介紹
簡介,術文,語譯算法,初始,計算,賈憲十進位制布位,楊輝算草,
簡介
術文
增乘開平方法,以商數乘下發遞增求之。商第一位。上商得數以乘下發為乘方。命上商除實。上商得數以乘下發入乘方。一退為廉,下法再退。
商第二位。商得數以乘下發為隅。命上商除實訖。以上商乘下法入隅,皆名曰廉。一退,下法再退,以求第三位商數。
商第三位。用法如第二位求之
語譯算法
初始
把待開方數賦值給變數實。
廉:0;
下法:以100為底,不大於實的最大幕數(主要是為了把實以每2個數分為一組設定)
商:0;
計算
步驟1:估商(x),求最大的整數x(商)使得:
(廉+x)*x <= 向下取整(實/下法), 0<=x<=9
(估出的x(商)即為開方後當前位的數值,)
步驟2:更新廉: 新廉=廉+x
步驟3:更新實: 新實=實-廉*x,若新實為0則表明開方完畢。
步驟4:再次更新廉:新廉=廉+x
步驟5:更新廉與下法:
新下法=下法/100(下法再退)
新廉=廉*10(與術文有差異,因為古法用算籌,現在用筆算,廉向下退一位,但相對於下法其實是進一位)
步驟6:以當前的 下法,廉,實 復上述步驟1~5,以求下一位的商,直到實=0或者達到要求的開方精度。
賈憲十進位制布位
- 算籌的布位。賈憲在紙上用書寫方式將算籌碼按十進位制布位。七萬一千八百二十四分寫兩行
 賈憲十進位算籌布位
賈憲十進位算籌布位下行的步、十、百、千、萬分離出來變為算籌的位值標籤;上行七一八二四成為十進位制數碼。
然後將算籌碼依次排在相應的位值標籤步、十、百、千、萬之下:
 賈憲十進位制布位
賈憲十進位制布位楊輝算草
楊輝以七萬一千八百二十四為例,列出詳細算草。 算草分四行,被除數放在第二行,稱為實,第一行是商,第四行為下法,第三行是廉。 將算籌放在第四行萬字之下。 賈憲增乘開平方動畫
賈憲增乘開平方動畫
 賈憲增乘開平方動畫
賈憲增乘開平方動畫
初始 |  楊輝算草 楊輝算草 |
計算(第一輪) | |
經過步驟1,2,3後的算籌結果: 1估計第一個商數得2,將安置在第一行百位置之上。 2將上商2乘下法1,得數2,放在第三行廉。 3跟新實,實-廉*商數*下法(算籌中廉數是乘下法後的數,所以不用再乘下法) 7-2*2=3 |  楊輝算草 楊輝算草 |
經過步驟4,5後的算籌結果: 4跟新廉=2+2=4 5下法與廉下移 退下法兩位,退廉1位 |  楊輝算草 楊輝算草 |
步驟6,進入第二輪計算商的下一位置,重複步驟1~5 | |
進過步驟1,2 1估商得6 2跟新廉:40+6=46 |  楊輝算草 楊輝算草 |
步驟3,跟新實 318-6*46=42 |  楊輝算草 楊輝算草 |
步驟4,更新廉 46+6=52 |  楊輝算草 楊輝算草 |
步驟5,6,並進入下一輪步驟1,2 5,更新下法與廉 退下法兩位,退廉1位 6,1估商為8 2,跟新廉:520+8=528 |  楊輝算草 楊輝算草 |
步驟3,跟新實後實為0,開方完畢 | 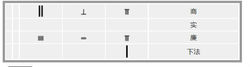 楊輝算草 楊輝算草 |
算草上的商即為開方後的結果:268 |
用增乘開平方法得到的解:


