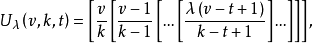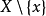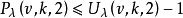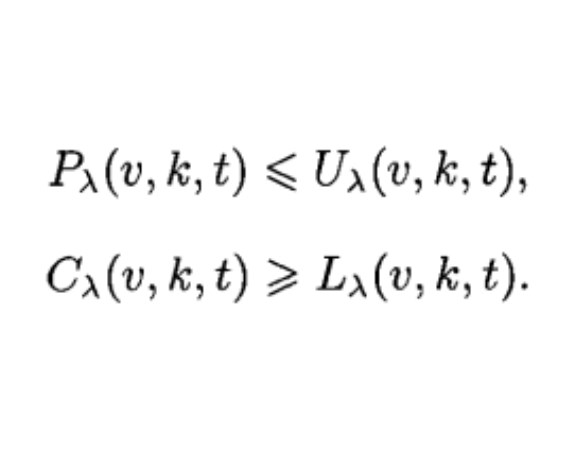填充設計

填充設計(packing design)是t設計的一種推廣，設X為v元集，B為X的某些k元子集的族，若X的任一t元子集至多包含在B的λ個成員(區組)中，則稱(X，B)為t-(v，k，λ)填充設計，t-(v，k，λ)設計也是一個填充設計。對給定的參數t，v，k，λ，使t-(v，k，λ)填充設計存在的最大區組數稱為填充數，記為D_λ(v，k，t)。填充設計對編碼理論有重要的套用，事實上，填充數D₁(v，k，2)就是字長v，極小距離為2(k-1)且碼字重量均為k的二元碼的最大碼字個數，當t=2及k=3，4時，填充數D_λ(v，k，t)的確切值已經得到。

基本介紹

• 中文名：填充設計
• 外文名：packing design
• 所屬學科：數學
• 所屬問題：組合學（組合設計理論）
• 簡介：t設計的一種推廣

基本介紹

定義 給定正整數t，v，k，λ，設X為一個v元集，A為由X的k元子集(稱為區組)所組成的子集族，若X的任意一個t元子集都至多包含在λ個區組中，則稱(X，A)為一個t-(v，k，λ)填充設計(packing design)。令

P_λ(v，k，t)={max b |存在區組數為b的t-(v，k，λ)填充設計)， (1)

P_λ(v，k，t)叫做填充數(packing number)。若(X，A)是區組數為P_λ(v，k，t)的t-(v，k，λ)填充設計，則叫做最大(或最優)t-(v，k，λ)填充設計，通常將P₁(v，k，t)記作P(v，k，t)。

例題解析

【例1】設X=Z₁₀，

A：{0，1，2，3}，{o，4，5，6}，{1，4，7，8}，{2，5，7，9}，{3，6，8，9}，

B：{0，1，2，9}，{0，3，4，8}，{0，5，6，7}，{1，2，3，4}，{1，2，5，6}，

{1，2，7，8}，{3，4，5，6}，{3，4，7，9}，{5，6，8，9}.

則(X,A)是一個2-(10，4，1)填充設計，(X，B)是一個2-{10，4，1}覆蓋設計，設A'為A的任一子集，則(X，A')也是2-(10，4，1)填充設計。設B'為在B中添加X的若干4元子集而得，則(X，B')也是2-(10，4，1)覆蓋設計。

【例2】若t-(v，k，λ)設計存在，則它既是最大t-(v，k，λ)填充設計，又是最小t-(v，k，λ)覆蓋設計。

設x為實數，用[x]表示不超過x的最大整數，[x]為不小於x的最小整數，令

當λ=1時，將U₁(v，k，t)記作U(v，k，t)，將L₁(v，k，t)記作L(v，k，t)。

相關定理

關於填充數P_λ(v，k，t)的上界和覆蓋數C_λ(v，k，t)的下界。我們有如下結果。

定理1(Schönheim界)

證明 顯然有

即當t=1時結論成立，今設t≥2，(X，A)為一個t-(v，k，λ)填充設計。對任意x∈X，A中包含x的全體區組去掉點x後作成上的一個填充設計，因此其區組數。因此有

,從而由式(3)及歸納法即得式(1)，同理可得

由式(4)及歸納法得式(2)，從而即得結論。

當t=2時，H.Hanani進一步證明了以下結論。

定理2 設。

(i)若，則

(ii)若，則