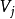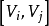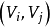運籌學中把一些研究對象用節點表示,對象之間的關係用連線邊表示。用點、邊的集合構成圖。圖論是研究有節點和邊所組成圖形的數學理論和方法。圖是網路分析的基礎,根據具體研究的網路對象(如:鐵路網、電力網、通信網等),賦予圖中各邊某個具體的參數,如時間、流量、費用、距離等,規定圖中各節點代表具體網路中任何一種流動的起點,中轉點或終點,然後利用圖論方法來研究各類網路結構和流量的最佳化分析。網路分析還包括利用網路圖形來描述一響工程中各項作業的進度和結構關係,以便對工程進度進行最佳化控制。
基本介紹
- 中文名:圖與網路分析
- 外文名:Graph and network analysis
- 領域:運籌學
- 關係:圖是網路分析的基礎
- 舉例:鐵路網、電力網、通信網等
- 相關名詞:網路最短路問題
圖論介紹,圖的基本概念,最短路問題,最大流問題,
圖論介紹
運籌學中把一些研究對象用節點表示,對象之間的關係用連線邊表示。用點、邊的集合構成圖。圖論是研究有節點和邊所組成圖形的數學理論和方法。圖是網路分析的基礎,根據具體研究的網路對象(如:鐵路網、電力網、通信網等),賦予圖中各邊某個具體的參數,如時間、流量、費用、距離等,規定圖中各節點代表具體網路中任何一種流動的起點,中轉點或終點,然後利用圖論方法來研究各類網路結構和流量的最佳化分析。網路分析還包括利用網路圖形來描述一響工程中各項作業的進度和結構關係,以便對工程進度進行最佳化控制。
圖的基本概念
圖是由點和點與點之間的連線組成。
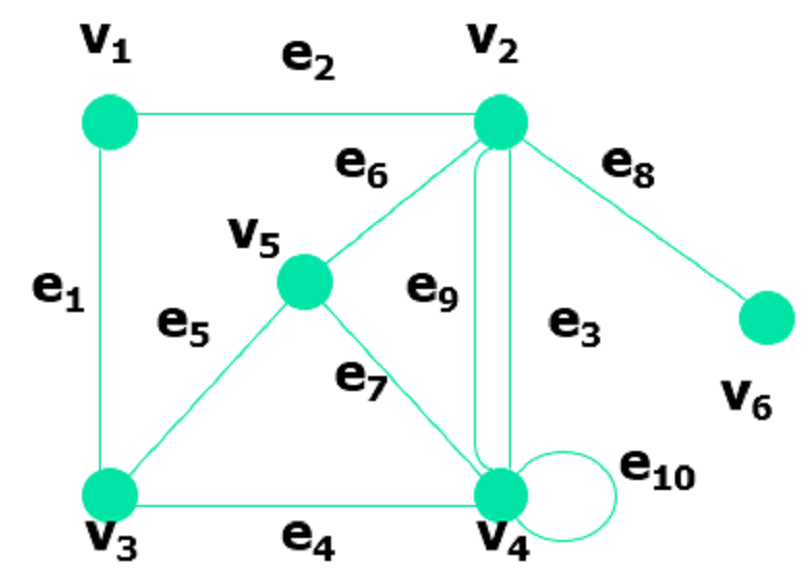
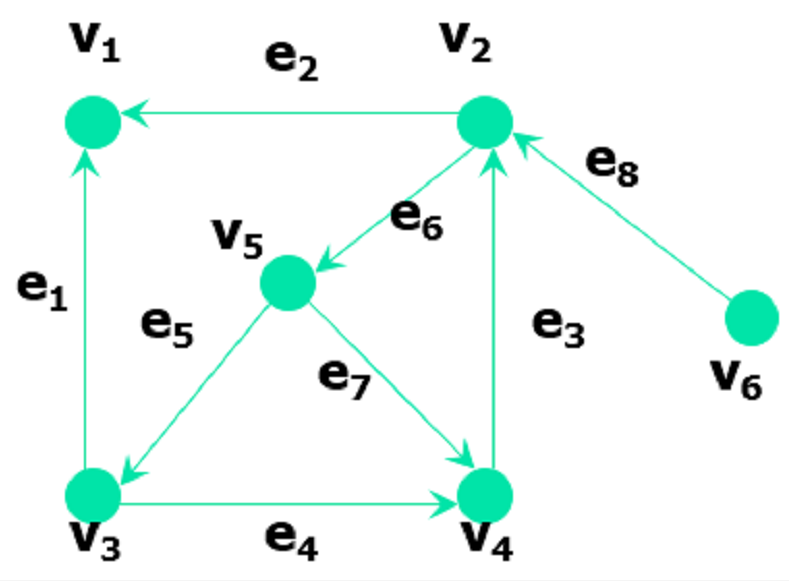
相鄰點:兩點之間的邊屬於E;
相鄰邊:如果兩條邊有一個公共端點;
環:邊的兩個端點相同;
多重邊(平行邊):兩個點之間有多於一條邊(弧);
多重圖: 無環但允許有多重邊的圖;
簡單圖:無環且無多重邊的圖;
註:在有向圖中,如果兩點之間有不同方向的兩條弧,不是多重邊。
端點的次d(v):點 v 作為端點的邊的個數;
奇點:d(v)=奇數; 偶點:d(v)=偶數;
懸掛點:d(v)=1;懸掛邊:與懸掛點連線的邊,
孤立點:d(v)=0;空圖: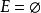 ,無邊圖。
,無邊圖。
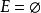
在有向圖中,以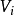 為始點的邊數稱為
為始點的邊數稱為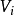 的出次,以
的出次,以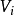 為終點的邊數稱為
為終點的邊數稱為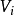 的入次,入次和出次的和稱為該點的次。
的入次,入次和出次的和稱為該點的次。
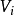
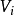
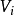
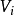
有向圖中所有頂點的入次之和等於所有頂點的的出次之和。
圖的連通性
通路:由兩兩相鄰的點及其相關聯的邊構成的點邊序列。如:
v0 , e1 , v1 , e2 , v2 , e3 , v3 , … , vn-1 , en , vn ,v0 , vn
分別為鏈的起點和終點。
簡單鏈:鏈中所含的邊均不相同。
初等鏈:鏈中所含的點均不相同,也稱通路。
圈:起點和終點相同的鏈。
迴路:通路的起點和終點相同
連通圖:圖中任意兩點之間均至少有一條鏈相連,否則稱作不連通圖。
任何一個不連通的圖都可以分為若干個連同子圖,每一個都稱為原圖的一個分圖。
連通是一個很重要的概念,如果一個問題所對應的圖是一個不連通圖,則該問題一定可以分解成互不相關的子問題來加以研究,即可以把不連通圖分解成連通的子圖來研究。
樹與部分樹
一個沒有圈的圖稱為一個無圈圖或稱為林。
一個連通的無圈圖則稱為樹,一個林的每個連通子圖都是一個樹。
若T是圖G=(V,E)的部分圖,且T是樹,則稱T為G的部分樹。
若T是圖G的部分樹,則從G中去掉T中所有的邊,所得到的子圖稱為G中的T的余樹,也稱為G的一個余樹。
余樹不一定是樹!
網路
點和邊帶有某種數量指標的圖稱為網路,或稱為賦權圖。
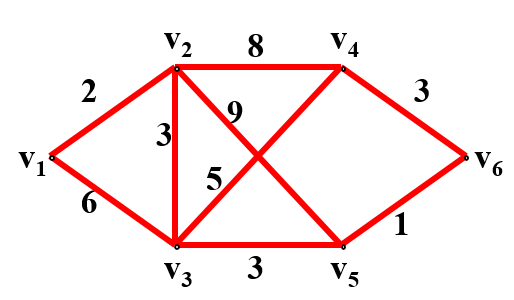
網路最小樹問題
最小樹問題:選取網路中的部分圖,使得網路連通,且使總權數最小。
在實際套用中,經常碰到需要求一個賦權連通圖的最小樹的問題。例如,用節點表示城市,用邊表示可以在兩個城市之間架設光纜,邊上的權表示光纜的長度,試求應如何架設光纜,才能使任意兩城市之間均由光纜相通,且使光纜的總長度最短。
求最小樹的方法,依據的是樹的特點,即無圈和連通,加上最短的要求,方法主要有兩種:一種稱為破圈法,一種稱為取邊避圈法。
(1)取邊避圈法 :
方法步驟:依次在圖中取一個權值最小的邊,或者是相對最短的邊,並且在每次取邊時都不能與已取的邊構成圈。
- 首先在圖中選最短的邊,並且將與之關聯的兩個點標記△;
- 然後每次都在標記點和未標記點間可能的邊中取一個最短的邊,並將新選的邊標記;
- 重複上述過程,直到所有的點均被標記了。
(2)破圈法:
方法步驟:
- 在網路圖中尋找一個圈,若已經無圈則轉步驟3。
- 在圈中選取權數最大的邊,從網路圖中截去該邊,對新的網路,轉步驟1。
- 若q=p-1(邊數=定點數-1),則已找到最小樹,否則網路圖不連通,無最小樹。
最短路問題
基本概念
網路:對有向圖D=(V,A),如果對於有向圖D中的每一條弧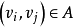 ,都有一個數
,都有一個數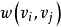 與它對應,此時稱D為一個網路,或稱賦權有向圖。
與它對應,此時稱D為一個網路,或稱賦權有向圖。
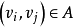
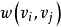
有向網路:網路中每個邊都是有向邊;
無向網路:網路中每個邊都是無向邊;
混合網路:網路中既有有向邊,又有無向邊;
網路最短路線問題:尋找網路中從起點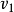 到終點
到終點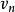 的最短路線。
的最短路線。
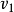
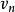
一般的最短路問題描述
給定一個賦權有向圖D=(V,A),對每一個弧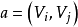 ,相應地有權
,相應地有權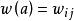 ,又給定D中的任何兩個頂點
,又給定D中的任何兩個頂點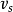 和
和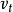 ,設P是從
,設P是從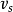 到
到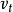 的路,定義路P的權是P中所有弧之和,記為
的路,定義路P的權是P中所有弧之和,記為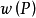 ,最短路問題就是要在所有從
,最短路問題就是要在所有從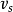 到
到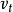 的路中,求一條權最小的路,即一條從
的路中,求一條權最小的路,即一條從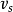 到
到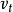 的路
的路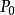 使得:
使得:
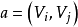
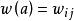
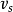
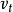
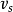
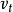
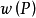
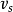
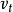
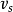
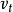
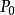
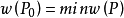
路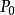 的權稱為從
的權稱為從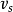 到
到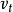 的距離,記為
的距離,記為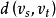 。
。
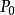
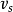
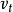
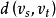
有向圖權值非負---- Dijkstra算法
Dijkstra算法的基本步驟(權值非負)
1.給頂點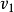 標號(0),
標號(0),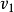 稱為已標號點,記標號點集為
稱為已標號點,記標號點集為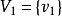 ;
;
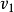
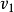
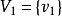
2.在未標號點集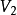 中找出與標號點集
中找出與標號點集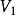 中的頂點
中的頂點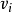 有弧相連(並且以
有弧相連(並且以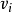 為起點)的點
為起點)的點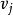 ;
;
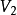
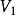
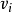
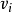
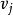
3.在第2步選出的點中,選出滿足下麵條件的點 ,並給
,並給 標號
標號 ,其中l為第一標號,
,其中l為第一標號,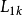 為第二標號。
為第二標號。



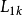
4.若最後一個頂點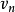 未標號,則轉回第2步;若
未標號,則轉回第2步;若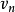 已標號,則從
已標號,則從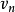 開始,按照第一個標號逆向追蹤,直到
開始,按照第一個標號逆向追蹤,直到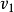 ,就得到從
,就得到從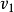 到
到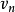 的最短路,
的最短路,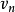 的第二個標號表示最短路的長度。
的第二個標號表示最短路的長度。
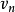
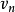
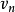
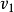
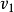
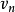
最大流問題
下圖表示從產地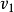 到銷地
到銷地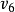 的交通網,弧旁邊的數字表示這條運輸線的最大通過能力,產品經過這個交通網從
的交通網,弧旁邊的數字表示這條運輸線的最大通過能力,產品經過這個交通網從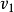 運到
運到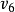 ,要求制定一個運輸方案使得從
,要求制定一個運輸方案使得從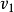 運到
運到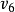 的產品數量最多。
的產品數量最多。
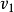
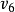
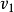
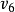
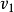
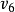

基本概念
網路與流:
對有向圖D=(V,A),如果其中指定某一點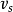 為發點,另一點
為發點,另一點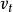 為收點,其他點則稱為中間點。若對於有向圖D中的每一條弧
為收點,其他點則稱為中間點。若對於有向圖D中的每一條弧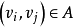 ,都有一個數
,都有一個數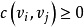 與它對應,稱c為弧的容量,記為D=(V,A,C)。
與它對應,稱c為弧的容量,記為D=(V,A,C)。
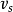
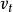
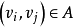
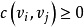
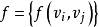
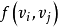
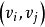
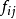
尋找最大流的標號法
網路D中的點分為兩類,一類是標號點(屬於 ),一類是非標號點(不屬於
),一類是非標號點(不屬於 ) ;
) ;


標號點有兩類一類是已檢查的,一類是未檢查的。每個標號點有兩個標號:第一個標號表示這個點的標號是從哪一點得到的,以便進一步找出增廣鏈,第二個標號是用來表示方向。
1.確定初始可行流
根據圖中弧的容量限制,確定一個初始的可行流,可以取零流。
2.標號過程
開始:由於始點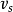 一定屬於
一定屬於 ,先給始點
,先給始點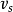 標上
標上 ,此時
,此時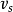 是標號但是未檢查的點,其他點都是未標號的點,選擇標號但是未檢查的點
是標號但是未檢查的點,其他點都是未標號的點,選擇標號但是未檢查的點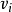 ,對於一切未標號的點
,對於一切未標號的點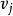 ,若在弧
,若在弧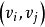 上,
上,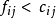 ,則給
,則給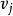 標號
標號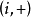 ,則
,則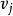 變為標號但是未檢查的點,否則不標號。若在弧
變為標號但是未檢查的點,否則不標號。若在弧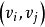 上,
上,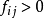 ,則給
,則給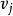 標號
標號 ,則
,則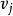 變為標號但是未檢查的點,否則不標號。
變為標號但是未檢查的點,否則不標號。
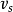

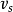

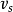
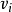
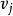
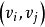
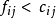
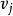
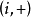
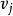
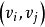
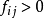
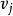

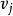



重複以上步驟,一旦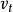 被標上號就得到了一條從
被標上號就得到了一條從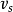 到
到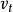 的增廣鏈
的增廣鏈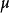 ,轉入調整過程。
,轉入調整過程。
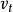
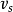
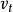
如果所有的標號都是已經檢查過的,但是標號過程無法進行下去,算法結束,此時的可行流就是最大流。