圓心角定理

圓心角定理,英文名為（The center angle theorem）。常用於數學計算，其主要功能用來計算相關圓的弧長問題。

基本介紹

• 中文名：圓心角定理
• 外文名：The central Angle theorem
• 條件：在同圓或等圓中
• 含義：相等的圓心角所對的弧相等

定理內容

在同圓或等圓中，相等的圓心角所對的弧相等，所對的弦相等，所對的弦心距也相等。

推理過程

根據旋轉的性質，將∠AOB繞圓心O旋轉到∠A'OB'的位置時，顯然∠AOB=∠A'OB'，射線OA與OA'重合，OB與OB'重合，而同圓的半徑相等，OA=OA'，OB=OB'，從而點A與A'重合，B與B'重合。

　因此，弧AB與弧A'B'重合，AB與A'B'重合。即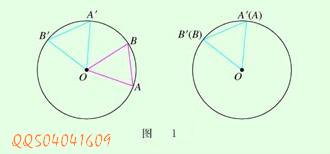

圓心角定理

弧AB=弧A'B'，AB=A'B'。

則得到上面定理。

同樣還可以得到：

在同圓或等圓中，如果兩條弧相等，那么他們所對的圓心角相等，所對的弦相等，所對的弦心距也相等。

在同圓或等圓中，如果兩條弦相等，那么他們所對的圓心角相等，所對的弧相等，所對的弦心距也相等。

所以，在同圓或等圓中，兩個圓心角、兩條弧、兩條弦中有一組量相等，它們所對應的其餘各組量也相等。

相關內容

垂徑定理、圓心角、弧、弦、弦心距間的關係

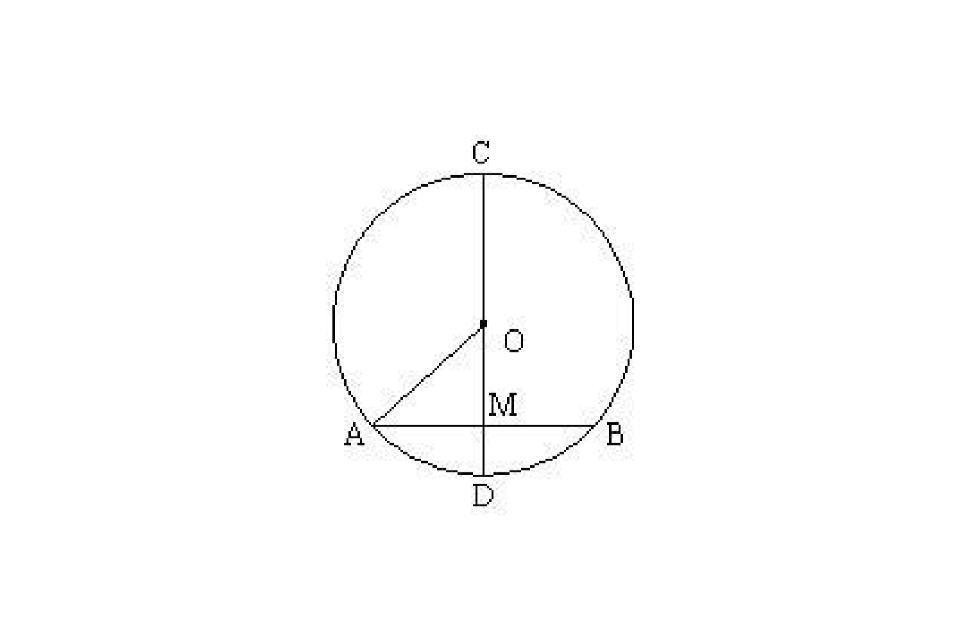
1. 理解由圓的軸對稱性推出垂徑定理，概括理解垂徑定理及推論為“知二推三”。（1）過圓心，（2）垂直於弦，（3）平分弦，（4）平分劣弧，（5）平分優弧。已知其中兩項，可推出其餘三項。注意：當知（1）（3）推（2）（4）（5）時，即“平分弦的直徑不能推出垂直於弦，平分兩弧。”而應強調附加“平分弦（非直徑）的直徑，垂直於弦且平分弦所對的兩弧”。

2. 深入理解垂徑定理及推論，為五點共線，即圓心O，垂足M，弦中點M，劣弧中點D，優弧中點C，五點共線。（M點是兩點重合的一點，代表兩層意義）

3. 套用以上定理主要是解直角三角形△AOM，在Rt△AOM中，AO為圓半徑，OM為弦AB的弦心距，AM為弦AB的一半，三者把解直角形的知識，借用過來解決了圓中半徑、弦、弦心距等問題。無該Rt△AOM時，注意巧添弦心距，或半徑，構建直角三角形。

圓圖

4. 弓形的高：弧的中點到弦的距離，明確由定義知只要是弓形的高，就具備了前述的（4）（2）或（5）（2）可推（1）（3）（5）或（1）（3）（4），實際可用垂徑定理及推論解決弓形高的有關問題。

5. 圓心角、弧、弦、弦心距四者關係定理，理解為：（1）圓心角相等，（2）所對弧相等，（3）所對弦相等，（4）所對弦的弦心距相等。四項“知一推三”，一項相等，其餘三項皆相等。源於圓的旋轉不變性。即：圓繞其圓心旋轉任意角度，所得圖形與原圖象完全重合。

6. 套用關係定理及推論，證角等，線段等，弧等，等等，注意構造圓心角或弦心距作為輔助線。

圓圖

7. 圓心角的度數與弧的度數等，而不是角等於弧。