圓周卷積定理

圓周卷積定理又稱循環卷積定理。對於時域圓周卷積，其含義為：兩序列離散傅立葉變換的乘積等於此兩序列的圓周卷積的離散傅立葉變換。對於頻域圓周卷積，其含義為：兩序列乘積的離散傅立葉變換等於兩序列離散傅立葉變換的圓周卷積除以圓周卷積列長的結果。

基本介紹

• 中文名：圓周卷積定理
• 外文名：Circular Convolution Theorem
• 別 名：循環卷積定理
• 學科領域：數位訊號處理

時域圓周卷積定理

兩序列離散傅立葉變換的乘積等於此兩序列的圓周卷積的離散傅立葉變換。利用離散傅立葉變換對表示為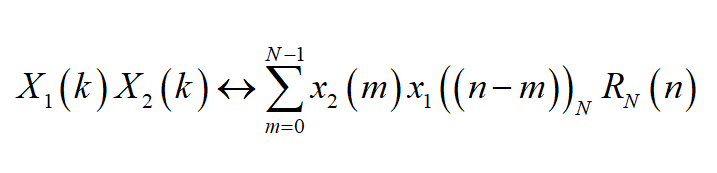

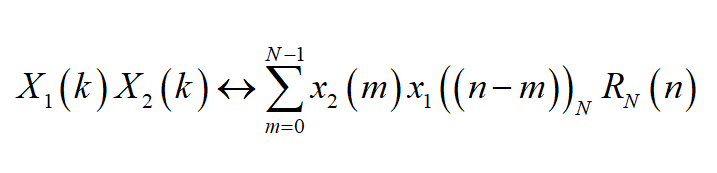
時域周期卷積定理

其中，變換對右邊式子可表示為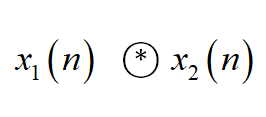

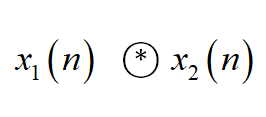
圓周卷積定理

即為圓周卷積的符號表示，對於頻域圓周卷積亦同，下文不再贅述。

頻域圓周卷積定理

兩序列乘積的離散傅立葉變換等於兩序列離散傅立葉變換的圓周卷積除以圓周卷積列長的結果。利用離散傅立葉變換對表示為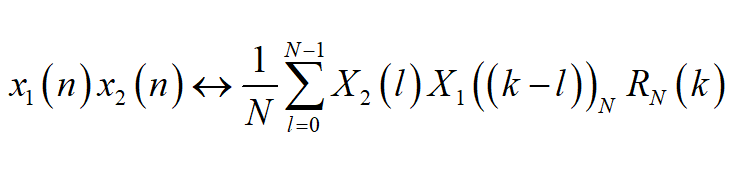

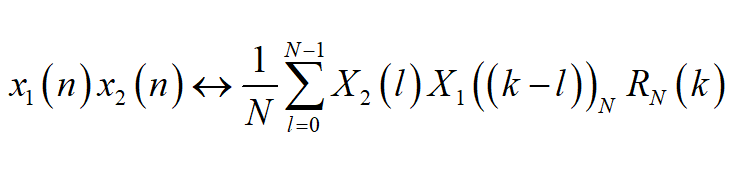
頻域周期卷積定理

圓周卷積和線性卷積的關係

實際數位訊號處理要求解線性卷積，而圓周卷積可以採用快速傅立葉變換（FFT）技術，適用於計算機快速計算的要求，故探究圓周卷積和線性卷積的關係，以及利用圓周卷積替代線性卷積而不失真的條件，尤為重要。

圓周卷積是周期卷積的取主值序列，而周期卷積是兩有限長序列（設序列長分別為M和N）線性卷積以L為周期的周期延拓。線性卷積具有N+M-1個非零序列值。因此，若周期卷積周期L＜N+M-1，則線性卷積的周期延拓就必然有一部分非零序列值要交疊起來，發生混淆。只有當L≥M+N-1時，才不至於發生交疊，此時周期卷積中的每一個周期L內，前N+M-1個序列值正是線性卷積的結果。綜上，要使圓周卷積與線性卷積相等而不產生混淆，必要條件是：L≥N+M-1。

圓周卷積的套用——計算無限長序列線性卷積

對於實際的數位訊號處理系統，設計有限長的系統序列是容易的，但是待處理的信號往往是近似無限長的，受計算機處理器字長限制，必須將信號序列分段進行快速卷積處理。設信號被等分為列長N的分段（N的取值最好與L取值的數量級相等），系統序列長為M，圓周卷積結果序列長為L。為使周期卷積周期L≥N+M-1，必須通過特定的方法延長信號序列和系統序列。按照延長序列的方法，可將卷積計算方法分為兩種：重疊相加法，重疊保留法。

重疊相加法

重疊相加法的含義與基本計算過程：卷積之前通過對分段信號序列（和系統序列）分別補零延長，使得L≥N+M-1；卷積之後作求和運算時，每段卷積最後M-1個點必定和下一段前M-1個點重疊，求和時這些重疊點的取值也要按位相加。因此，該方法稱為重疊相加法。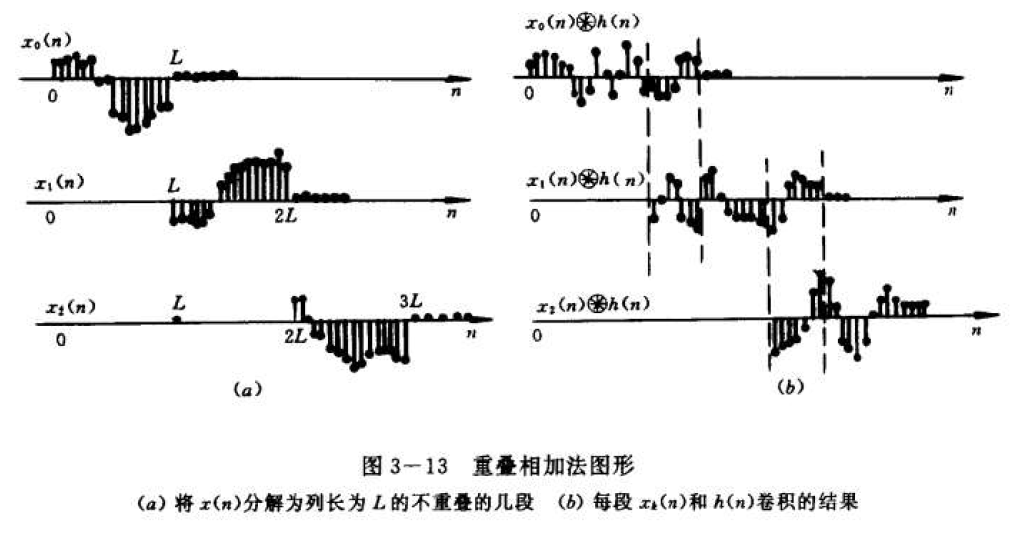

重疊相加法

重疊保留法

重疊保留法的含義與基本計算過程：卷積之前通過保留分段信號序列前端M-1位原輸入序列（第一段前M-1為置零），使分段信號序列延長直至滿足L≥N+M-1（系統序列長保持不變）；卷積之後作求和運算時，捨棄每段卷積結果前M-1位的錯誤取值序列後按位相加，相加時則不存在重疊的點。該方法在卷積前保留了冗餘位輸入數據，卷積後又為避免無效數據重疊相加而捨去，故稱為重疊保留法。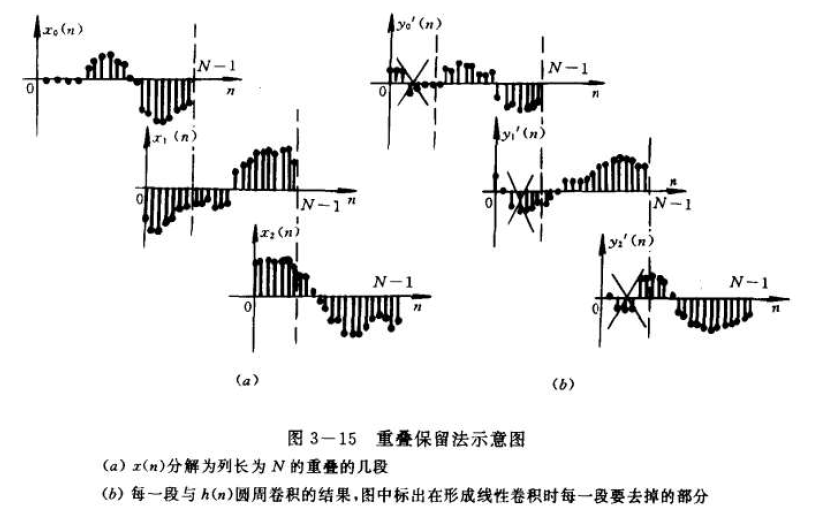

重疊保留法