回溯算法實際上一個類似枚舉的搜尋嘗試過程，主要是在搜尋嘗試過程中尋找問題的解，當發現已不滿足求解條件時，就“回溯”返回，嘗試別的路徑。回溯法是一種選優搜尋法，按選優條件向前搜尋，以達到目標。但當探索到某一步時，發現原先選擇並不優或達不到目標，就退回一步重新選擇，這種走不通就退回再走的技術為回溯法，而滿足回溯條件的某個狀態的點稱為“回溯點”。許多複雜的，規模較大的問題都可以使用回溯法，有“通用解題方法”的美稱。
基本介紹
- 中文名：回溯算法
- 外文名：backtracking algorithm
- 其他名稱：試探法
- 方法：一種系統地搜尋問題的解
- 基本思想：能進則進
- 例題：八皇后問題
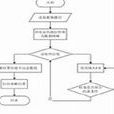
來源,基本思想,算法框架,典型例題,問題描述,代碼,
來源
回溯算法也叫試探法，它是一種系統地搜尋問題的解的方法。
用回溯算法解決問題的一般步驟：
1、 針對所給問題，定義問題的解空間，它至少包含問題的一個（最優）解。
2 、確定易於搜尋的解空間結構,使得能用回溯法方便地搜尋整個解空間 。
3 、以深度優先的方式搜尋解空間，並且在搜尋過程中用剪枝函式避免無效搜尋。
確定了解空間的組織結構後，回溯法就從開始結點（根結點）出發，以深度優先的方式搜尋整個解空間。這個開始結點就成為一個活結點，同時也成為當前的擴展結點。在當前的擴展結點處，搜尋向縱深方向移至一個新結點。這個新結點就成為一個新的活結點，並成為當前擴展結點。如果在當前的擴展結點處不能再向縱深方向移動，則當前擴展結點就成為死結點。此時，應往回移動（回溯）至最近的一個活結點處，並使這個活結點成為當前的擴展結點。回溯法即以這種工作方式遞歸地在解空間中搜尋，直至找到所要求的解或解空間中已沒有活結點時為止。
基本思想
回溯算法的基本思想是：從一條路往前走，能進則進，不能進則退回來，換一條路再試。八皇后問題就是回溯算法的典型，第一步按照順序放一個皇后，然後第二步符合要求放第2個皇后，如果沒有位置符合要求，那么就要改變第一個皇后的位置，重新放第2個皇后的位置，直到找到符合條件的位置就可以了。回溯在迷宮搜尋中使用很常見，就是這條路走不通，然後返回前一個路口，繼續下一條路。回溯算法說白了就是窮舉法。不過回溯算法使用剪枝函式，剪去一些不可能到達 最終狀態（即答案狀態）的節點，從而減少狀態空間樹節點的生成。回溯法是一個既帶有系統性又帶有跳躍性的的搜尋算法。它在包含問題的所有解的解空間樹中，按照深度優先的策略，從根結點出發搜尋解空間樹。算法搜尋至解空間樹的任一結點時，總是先判斷該結點是否肯定不包含問題的解。如果肯定不包含，則跳過對以該結點為根的子樹的系統搜尋，逐層向其祖先結點回溯。否則，進入該子樹，繼續按深度優先的策略進行搜尋。回溯法在用來求問題的所有解時，要回溯到根，且根結點的所有子樹都已被搜尋遍才結束。而回溯法在用來求問題的任一解時，只要搜尋到問題的一個解就可以結束。這種以深度優先的方式系統地搜尋問題的解的算法稱為回溯法，它適用於解一些組合數較大的問題。
算法框架
（pascal語言）
procedure try(i:integer);varbeginif i>n then 輸出結果else for j:=下界 to 上界 dobeginx[i]:=h[j];if 可行{滿足限界函式和約束條件} then begin 置值；try(i+1); end;end;（c++）以下以一道題目為例，素數環問題
將從1到n這n個整數圍成一個圓環，若其中任意2個相鄰的數字相加，結果均為素數，那么這個環就成為素數環。
#include<iostream>#include<cmath>#include<cstdio>using namespace std;int ans[21] = {0}, tot = 0;bool a[21] = {0};void print(){tot++;cout << "No." << tot << ':';for (int i = 1; i <= 20; i++)cout << ans[i] << ' ';cout << endl;}bool isprime(int x1, int x2){int i = x1 + x2,f;for (f = 2; f <= sqrt(i); f++)if (i % f == 0)return false;return true;}int search(int t){for (int i = 1; i <= 20; i++){if (a[i] == false && isprime(ans[t - 1], i)){ans[t] = i;a[i] = true;if (t == 20 && isprime(ans[1], ans[20]))print();elsesearch(t + 1);a[i] = false;}}}int main() {search(1);printf("The total is %d", tot);}典型例題
問題描述
八皇后問題：在8×8格的西洋棋上擺放八個皇后，使其不能互相攻擊，即任意兩個皇后都不能處於同一行、同一列或同一斜線上，問有多少種擺法。
代碼
int g_number = 0; void EightQueen(){ const int queens = 8; int ColumnIndex[queens]; for(int i = 0; i < queens; ++ i) ColumnIndex[i] = i; Permutation(ColumnIndex, queens, 0);} void Permutation(int ColumnIndex[], int length, int index){ if(index == length) { if(Check(ColumnIndex, length)) { ++ g_number; PrintQueen(ColumnIndex, length); } } else { for(int i = index; i < length; ++ i) { int temp = ColumnIndex[i]; ColumnIndex[i] = ColumnIndex[index]; ColumnIndex[index] = temp; Permutation(ColumnIndex, length, index + 1); temp = ColumnIndex[index]; ColumnIndex[index] = ColumnIndex[i]; ColumnIndex[i] = temp; } }} bool Check(int ColumnIndex[], int length){ for(int i = 0; i < length; ++ i) { for(int j = i + 1; j < length; ++ j) { if((i - j == ColumnIndex[i] - ColumnIndex[j]) || (j - i == ColumnIndex[i] - ColumnIndex[j])) return false; } } return true;} void PrintQueen(int ColumnIndex[], int length){ printf("Solution %d\n", g_number); for(int i = 0; i < length; ++i) printf("%d\t", ColumnIndex[i]); printf("\n");}