四次不定方程是一類著名的不定方程。關於四次不定方程整數解的研究,是個難度較大的數論專題。四次不定方程的結果仍然較多地是二元和三元的情形,即使是二元的情形,四次不定方程的問題也並不簡單。
基本介紹
- 中文名:四次不定方程
- 外文名:quartic indeterminate equation
- 適用範圍:數理科學
簡介,發展歷史,無窮遞降法,
簡介
四次不定方程是一類著名的不定方程。關於四次不定方程整數解的研究,是個難度較大的數論專題。目前的研究主要在二元四次和三元四次方面有一些結果,其餘都還在探索之中。
發展歷史
在兩百多年以前就已經知道不定方程 有兩組整數解
有兩組整數解 。
。


直到1942年,永格倫(Ljunggren,W.)才給出了一個很繁瑣的方法,證明了方程 除上述兩組解之外,再沒其他正整數解。
除上述兩組解之外,再沒其他正整數解。

17世紀,費馬(Fermat,P.de)證明了不定方程 沒有
沒有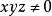 的整數解,利用科恩(Cohen,J.H.E.)關於斐波那契數列的兩個重要結果,可以證明下列不定方程解的情況為:
的整數解,利用科恩(Cohen,J.H.E.)關於斐波那契數列的兩個重要結果,可以證明下列不定方程解的情況為: ,僅有兩組整數解
,僅有兩組整數解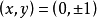 ;
; ,僅有四組整數解
,僅有四組整數解 ;
;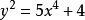 ,僅有十組整數解
,僅有十組整數解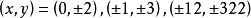 ;
; ,僅有八組整數解
,僅有八組整數解 。
。

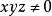

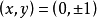


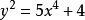
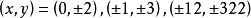


更一般的結果是:設整數D>1,且無平方因子,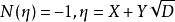 是
是 中的基本單位數,若X,Y不是整數,則不定方程
中的基本單位數,若X,Y不是整數,則不定方程 當D=5時,僅有一組正整數解
當D=5時,僅有一組正整數解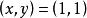 ;當D=13時,僅有一組正整數解
;當D=13時,僅有一組正整數解 。如果D是除5和13以外的奇素數時,則不定方程
。如果D是除5和13以外的奇素數時,則不定方程 無正整數解。當D=5時,方程僅有兩組正整數解
無正整數解。當D=5時,方程僅有兩組正整數解 ;當D=13時,方程僅有一組正整數解
;當D=13時,方程僅有一組正整數解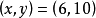 。
。
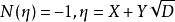


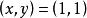



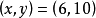
無窮遞降法
證明如下:
設 中有一組
中有一組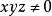 的解,且設x>0,y>0,z>0,x是所有解中最小的。顯然,
的解,且設x>0,y>0,z>0,x是所有解中最小的。顯然, 。
。

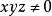

如果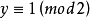 ,則由
,則由 得出
得出 ,故有
,故有 ,得出
,得出 的一組解
的一組解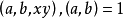 ,而0<a<x,與x最小矛盾。
,而0<a<x,與x最小矛盾。
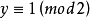




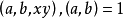
如果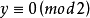 ,則
,則 。不失一般,可設
。不失一般,可設 ,
, ,則有
,則有 ,故
,故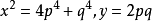 ,因此
,因此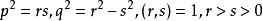 ,又得
,又得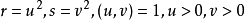 ,則有
,則有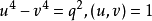 ,而
,而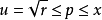 ,仍與x最小矛盾。
,仍與x最小矛盾。
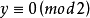




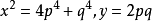
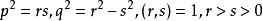
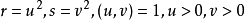
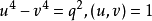
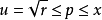
這就證明了 沒有
沒有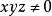 的整數解。證畢。
的整數解。證畢。