喬姆斯基層次結構

可計算枚舉語言被命名為0-型語言，上下文相關語言被命名為1-型語言，上下文無關語言被命名為2-型語言，正則語言被命名為3-型語言。低型語言不是高型的，默認情況下，每個高型的語言都是低型的，這個被稱為喬姆斯基層次結構。

基本介紹

• 中文名：喬姆斯基層次結構
• 外文名：Chomsky hierarchy
• 層次：1-型、2-型、3-型、0-型
• 系統：計算機
• 定義：低級語言不是高型
• 套用學科：計算機原理

結構簡介

存在正則語言的一個擴展。在正則語言裡，一個非終結符號可以像串最右端符號那樣出現任一生成式的右邊。這種語法也叫作右線性語法(right linear grammars)。當語法中每個生成式最多有一個非終結符在它右邊，並且非終結符像最左端符號那樣出現左邊時，語法叫作左線性語法(1eft linear grammar)。線上性語法中，每個生成式在右邊之多有一個非終結符，在位置上則無任何限制。

可以證明，線性語言，即由線性語法生成的語言，形成了上下文無關語言的一個子集。

很顯然，每個正則語言都是線性的。線性語言類與確定性上下文無關語言不同。這些結果總結起來叫作喬姆斯基層次結構(Chomsky’s Hierarchy)。它規定：

每一個正則語言都是線性的。

每一個正則語言都是確定性上下文無關的。

每一個線性語言都是上下文無關的。

每一個確定性上下文無關語言都是上下文無關的。

每一個上下文無關語言都是上下文相關的。

每一個上下文相關語言都是可判定的。

每一個可判定語言都是可計算枚舉的。

此外，先前說明的語言類之間的包含關係是固有的。其意味著：

存在可計算枚舉語言是不可判定的。

存在可判定語言是非上下文相關的。

存在上下文相關語言是非上下文無關的。

存在上下文無關語言不是確定性上下文無關的。

存在上下文無關語言不是線性的。

存在確定性上下文無關語言不是正則的。

存線上性語言不是正則的。

存在確定性上下文無關語言不是線性的。

存線上性語言不是確定性上下文無關的。

線性有界自動機是非確定性圖靈機帶上線性空間的約束。相似的約束在確定性圖靈機上隨之產生了所謂的確定性線性有界自動機(deterministic linear bounded automata)。還未知的是，確定性線性有界自動機接受語言是否構成那些(非確定性)線性有界自動機接受語言的子集。

設定一個字母表三。設RE，REC，CS，CF，LIN，DCF，REG各自分別表示語言類包括三上所有可計算枚舉(遞歸可枚舉的)、可判定(遞歸)、上下文相關、上下文無關、線性、確定性上下文無關，和正則語言。喬姆斯基層次結構可以寫成更進一步地，正則語言那些能被有限自動機接受的；上下文無關語言是那些被疊加自動機接受的；上下文相關語言是那些被線性有界自動機接受的；可計算枚舉語言是那些被圖靈機接受的。

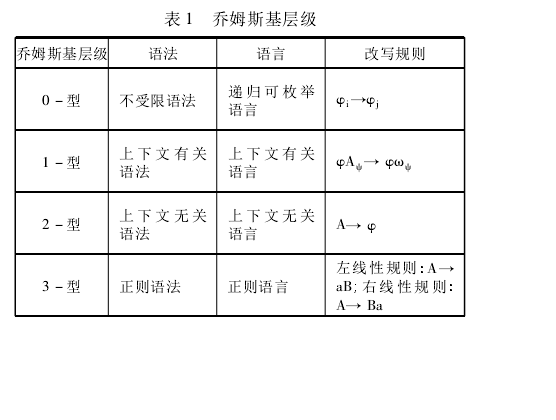
由於這個層次結構，可計算枚舉語言被命名為0-型語言，上下文相關語言被命名為1-型語言，上下文無關語言被命名為2-型語言，正則語言被命名為3-型語言。低型語言不是高型的，默認情況下，每個高型的語言都是低型的。這個被稱為喬姆斯基層次結構，而上述闡明的結果構成了擴展的喬姆斯基層次結構。

喬姆斯基形式文法

在計算機科學中，形式語言是某個字母表上一些有限長字串的集合，而形式文法是描述這個集合的一種方法。形式文法之所以這樣命名，是因為它與人類自然語言中的文法相似的緣故。最常見的文法的分類系統是喬姆斯基(Chomsky N)於1950年發展的喬姆斯基譜系，這個分類譜系把所有的文法分成四種類型：短語結構文法、上下文有關文法、上下文無關文法和正規文法。任何語言都可以由無限制文法來表達，餘下的三類文法對應的語言類分別是遞歸可枚舉語言、上下文無關語言和正規語言。依照排列次序，這四種文法類型依次擁有越來越嚴格的產生式規則，所能表達的語言也越來越少。儘管表達能力比短語結構文法和上下文相關文法要弱，但由於能高效率的實現，上下文無關文法和正規文法成為四類文法中最重要的兩種文法類型。

短語結構文法

短語結構文法是一種非受限文法，也稱為0型文法，是形式語言理論中的一種重要文法。一個四元組G=(∑，V，S，P)，其中∑是終結符的有限字母表，V是非終結符的有限字母表，S(∈V)是開始符號，P是生成式的有限非空集，P中的生成式都為a的形式，這裡d∈(∑∪V) * v(∑∪V) * ， ∈(∑∪V) *。短語結構文法又稱為0型文法。因對a和不加任何限制，故也稱其為無限制文法。0型文法生成的語言類與圖靈機接受的語言類相同，稱為0型語言類(常用L。表示)或遞歸可枚舉語言類(常用Lre表示)。

短語結構文法的標準型為：A→ξ，A→BC，A→∧，AB→CD，其中ξ∈(∑∪V)，A，B，C，D∈v，∧是空字。

對短語結構文法中的生成式作某些限制，即得到上下文有關文法、上下文無關文法和正則文法。

上下文有關文法

上下文有關文法是形式語言理論中的一種重要文法。一個四元組G=(∑，V，S，P)，其中∑是終結符的有限字母表，V是非終結符的有限字母表，S(∈V)是開始符號，P是生成式的有限非空集，P中的生成式都為的形式，這裡A∈V，a，∈(∑∪V) *，y∈(∑∪V) +。上下文有關文法又稱為1型文法。其生成式的直觀意義是：在左有a,右有的上下文中，A可以被所替換。上下文有關文法所生成的語言稱為上下文有關語言或1型語言。常用表示1型語言類。

上下文有關文法的標準型為：Aξ，ABC。ABCD，其中ξ∈(∑∪V)，A，B，C，D∈V。上下文有關語言類與線性有界自動機接受的語言類相同。

上下文無關文法

上下文無關文法是形式語言理論中一種重要的變換文法，在喬姆斯基分層中稱為2型文法，生成的語言稱為上下文無關語言或2型語言，在程式設計語言的語法描述中有重要套用。

上下文無關文法(簡稱CFG)可以化為兩種簡單的範式之一，即任一上下文無關語言(簡稱CFL)可用如下兩種標準CFG的任意一種生成：其一是喬姆斯基範式，它的產生式均取ABC或Aa的形式；其二是格雷巴赫範式，它的產生式均取AaBC或Aa的形式。其中A，B，C∈V，是非終結符；a∈∑，是終結符；a∈∑*，是終結符串。

從文法生成語言，可有多種推導方式。例如文法{SAB，Aa，Bb)可有兩種推導：S=>AB=>aB=>ab及S=>AB=>Ab=>ab。若每次都取最左邊的非終結符進行推導，如上例中的前一種方式那樣，則稱為左推導。如果有兩種不同的左推導推出同一結果，則稱此文法是歧義的，反之是無歧義文法。對有些歧義文法，可找到一個等價的無歧義文法，生成同一個語言。不具有無歧義文法的語言稱為本質歧義性語言。例如，{SA，Sa，Aa}是歧義的文法。。接受CFL的自動機稱為下推自動機。確定型和不確定型下推自動機接受的語言分別稱為確定型CFL和不確定型CFL，前者是後者的真子集。

正則文法

正則文法來源於20世紀50年代中期喬姆斯基對自然語言的研究，是喬姆斯基短語結構文法分層里的3型文法。正則文法類是上下文無關(2型)文法類的真子類，已套用於電腦程式語言編譯器的設計、詞法分析(文本處理中描述觸發過程動作的文本模式、檔案類型和掃描器、文本工具的標準基礎)、開關電路設計、句法模式識別等，是計算機和信息科學、工程、物理、化學、生物、醫學、套用數學不可忽視的論題。

正則文法有多種等價的定義，可以用“左線性文法”或者“右線性文法”來等價地定義正則文法。“左線性文法”要求產生式的左側只能包含一個非終結符號，產生式的右側只能是空串、一個終結符號或者一個非終結符號後隨一個終結符號。“右線性文法”要求產生式的左側只能包含一個非終結符號，產生式的右側只能是空串、一個終結符號或者一個終結符號後隨一個非終結符號。