哈德曼一格羅布曼定理(Hartman-Grobman the-orem)是關於雙曲奇點鄰域軌道分布性態的一個重要定理。
設O為
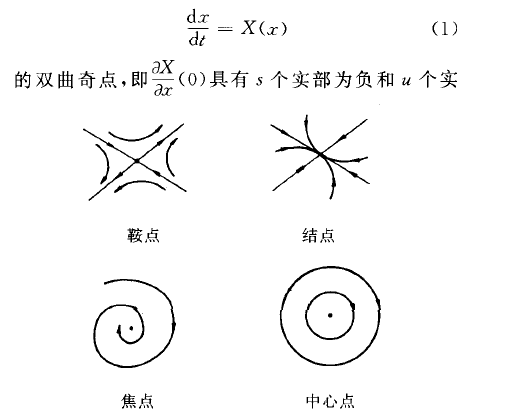
部為正的特徵值,s+u=n,則存在O的鄰域U,使在其內分別有、,u維流形E',E0,R"'門U=E.,印E0,對E'內的任一lim }p}(x)=0,而對E0內的任一點x lim}p}(x)=0.分別稱E'` , E“為奇點O的局部穩定和不穩定流形.當u=0時,稱奇點O為淵;當、一0時,稱奇點O為源.當n=2時,(1>為平面系統,O的幾何性態可由二階方陣嘗(0)的特徵值、m }z的不同情況來決定:若}i,a:為異號實數,則稱O為鞍點;若}i , }z為同號實數,則稱O為結點;若}i,}z為一對共扼複數,則稱O為焦點.在結點和焦點的情況,如.1,G0或a,}0,則相應奇點為穩定或不穩定的.若又,,又2為一對純虛根(非雙曲奇點),則0可能為中心點,也可能為焦點須進一步由(u的右端的非線性項的情況來具體確定.平面初等奇點的結構如圖所示.
