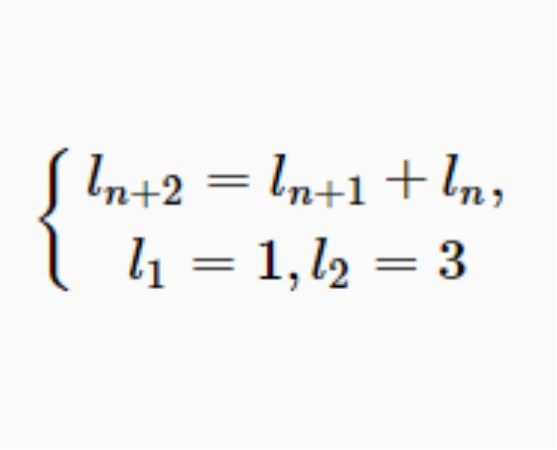呂卡數

呂卡數(Lucas number)是一類組合數，由F₁=1， F₂=3， F_n=F_n-1+F_n-2所確定的數列{F_n|n=1，2，3，…}的每個數F_n都稱為呂卡數，前幾個呂卡數是F₁=1，F₂=3，F₃=4，F₄=7，F₅=11，F₆=18等。

基本介紹

• 中文名：呂卡數
• 外文名：Lucas number
• 所屬學科：數學（組合學）
• 簡介：一類組合數
• 提出者：法國數學家呂卡(F.E.A.Lucas)
• 相關概念：斐波那契數列

基本介紹

法國數學家呂卡(F.E.A.Lucas，1842-1891)對斐波那契數列只作了極為微小的改變，就構造出嶄新的數列{l_n}，由遞歸方程

定義數列稱為呂卡(Lucas)數列(簡稱L-數列)，數列中的每個數都稱為呂卡數。

L-數列的前若干項為

1，3，4， 7， 11， 18， …

L-數列與斐波那契數列（下文簡稱F-數列）有相同的遞歸方程(但兩者的始值不同)，因而有相同的特徵方程和特徵根α，β，且不難證明L-數列的通項公式為

即

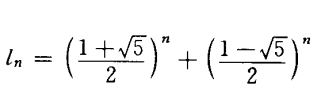
公式

相關性質

L-數列有與F-數列類似的一些性質。首先，L-數列與F-數列有相同的遞歸方程，所以F-數列的只涉及遞歸方程的性質對於L-數列都成立。特別地，奇階或偶階(即下標為奇數或偶數)的L-數列都有相同的遞歸方程

其次，與F-數列的Cassini恆等式類似，有下面的公式

呂卡數列有以下命題：

以下{u_n}為斐波那契數列，u_i(i=1,2,...)。

以下性質剛好可用斐氏數及呂卡數拼成正方形。

（圖1）

（圖2）

（圖3）

（圖4）

（圖5）

（圖6）