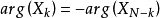同址計算

同址計算(Identical Address Operation)是FFT中的主要算法，因其在計算時總是用當前層替代前一層,具有地址不變的關係而得名。也就是輸出數據使用原輸入數據結點所占用的記憶體，輸出、輸入數據利用同一記憶體單元的這種蝶形計算稱為同址計算，該算法在計算全部分析點數據時具有很高的效率。

基本介紹

• 中文名：同址計算
• 外文名：Identical Address Operation
• 一級學科：信息與通信工程
• 二級學科：信號與信息處理
• 優點：節省存儲單元
• 缺點：計算局部譜線時存在冗餘

算法描述

為描述清楚起見，對右圖作一些約定：規定從左到右每一列為一層，用m(m=1,⋯,L)表示。節點所在行從上到下每一行為一個自然序號用k(k=0,⋯,N-1)表示，這樣節點就表示第m層的第k個節點，習慣上將第一列和最後一列的層下標省去，分別表示為和。

“同址運算”疊代算法是從第一層開始，以m層的各個節點Xm,k作為已知點，將(m+1)層的各個節點Xm+1,k疊代出來，直到算出最後一層為止，為了節省存儲空間，將已算得的對應節點數據替換前一節點，對應數據作為下一輪疊代的已知數據，“同址運算”由此得名。

算法優點

首先，該算法容易實現，利用旋轉因子中出現1處進行基分解(split-radix)省去複數乘積而使DFT速度進一步提高，該算法在計算全部譜線時效率很高。

其次，每一級的蝶形的輸入與輸出在運算前後可以存儲在同一地址的存儲單元中，這種同址運算的優點是可以節省存儲單元，從而降低對計算機存儲量的要求或降低硬體實現的成本。

算法缺點

雖然該算法在計算全部譜線時效率很高,但是在計算局部譜線時存在冗餘。

分析FFT結果的特點可知X(k)與X(N-k)有如下關係：

上式表明對N點的FFT只要求出(0-N/2)點,利用對偶規則可以得到另外一半,而不必算出全部點，因此存在冗餘。