基本介紹
- 中文名：史密夫圖表
- 外文名：Smith chart
- 又稱：史密斯圓圖
- 用途：傳輸線的阻抗匹配上
- 套用學科：電信
簡介,特點,算式,圓圖意義,基本意義,注意事項,阻抗匹配,匹配條件,方法,
簡介
史密夫圖表(Smith chart，又稱史密斯圓圖)是在反射系散平面上標繪有歸一化輸入阻抗（或導納）等值圓族的計算圖。是一款用於電機與電子工程學的圖表，主要用於傳輸線的阻抗匹配上。該圖由三個圓系構成，用以在傳輸線和某些波導問題中利用圖解法求解，以避免繁瑣的運算。一條傳輸線(transmission line)的電阻抗力(impedance)會隨其長度而改變，要設計一套匹配(matching)的線路，需要通過不少繁複的計算程式，史密夫圖表的特點便是省略一些計算程式。
特點
該圖表是由菲利普·史密斯(Phillip Smith)於1939年發明的，當時他在美國的RCA公司工作。一年後，一位名為Kurakawa的日本工程師也聲稱發明了這種圖表。史密斯曾說過，“在我能夠使用計算尺的時候，我對以圖表方式來表達數學上的關聯很有興趣”。
由於採用了歸一化措施，所以適用於任何特性阻抗和任意波長。精度則取決於圓圖的刻度。
阻抗圓圖由等電阻 （Ri）圓系、等電抗Xi圓系和|Γ|圓系構成，見圖1。其中Ri和Xi分別是歸一化輸入阻抗
的實部和虛部，
。
圖1 史密斯圓圖|Γ|是反射係數Γ的模。為避免圖上線條太多，|Γ|圓系一般不畫出。
史密斯圓圖的用途是多方面的：根據歸一化負載阻抗ZL/ZC，可求得反射係數Γ，在Γ=|Γ|∠θ已知的情況下可得到ZL/ZC。當ZL/ZC、歸一化長度(1/λ)巳知時可查出Zin/ZC。在Zin/ZC和歸一化長度已知時可得到ZL/ZC，而當Zin/ZC和ZL/ZC已知時可求出這段傳輸線的長度。在駐波比及第一個電壓最小點到傳輸線終端的距離已知時，利用此圖可以查出的ZL/ZC數值。
導納圓圈由等電導 （Gi）圓系、等電納 （Bi）圓系和|Γ|圓系構成。其中，Gi及Bi分別為歸一化輸入導納Yin/YC的實部和虛部。
導納圓圖與阻抗圓圖的形式一樣，只是阻抗圓圖中的Ri、Xi由Gi、Bi替代。常用於並聯電路的計算。
算式
史密斯圖表的基本在於以下的算式
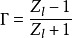
當中的Γ代表其線路的反射係數(reflection coefficient)，即S參數（S-parameter）里的S11，ZL是歸一負載值，即ZL / Z0。當中，ZL是線路本身的負載值，Z0是傳輸線的特徵阻抗（本徵阻抗）值，通常會使用50Ω。
圖表中的圓形線代表電阻抗力的實數值，即電阻值，中間的橫線與向上和向下散出的線則代表電阻抗力的虛數值，即由電容或電感在高頻下所產生的阻力，當中向上的是正數，向下的是負數。圖表最中間的點(1+j0)代表一個已匹配(matched)的電阻數值(ZL)，同時其反射係數的值會是零。圖表的邊緣代表其反射係數的長度是1，即100%反射。在圖邊的數字代表反射係數的角度(0-180度)和波長(由零至半個波長)。
有一些圖表是以導納值(admittance)來表示，把上述的阻抗值版本旋轉180度即可。
自從有了計算機後，此種圖表的使用率隨之而下，但仍常用來表示特定的資料。對於就讀電磁學及微波電子學的學生來說，在解決課本問題仍然很實用，因此史密夫圖表仍是重要的教學用具。
在學術論文裡，量度儀器的結果也常會以史密夫圖表來表示。
圓圖意義
基本意義
1.阻抗圓的上半圓內，x>0，其電抗為感抗，下半圓內，x<0，其電抗為容抗。
2.阻抗圓圖的實軸x = 0，實軸上每一點對應的阻抗都是純電阻，稱為純電阻線。
3.
的圓，r = 0，其上對應的阻抗都是純電抗，稱為純電抗圓。
4.實軸左端點，即左實軸與的圓的交點，z=0，代表阻抗短路點，而右實軸與 的圓的交點，即右端點，z = ，代表開路點。圓圖中心z=1，
，
= 1，稱為阻抗匹配點。
5.等R線：其軌跡為一族圓，圓心坐標為(
)，半徑為1/(r+1)。
6.等X線：其軌跡為一族圓，圓心坐標為(1，1/x)，半徑為1/x。
注意事項
1. 旋轉的方向問題：傳輸線由負載向電源方向移動（l 增大），在圓圖上應順時針方向旋轉；反之，由電源向負載方向移動（l減小），則應逆時針方向旋轉。
2. 反射係數值圓圖上未標出，計算時需將半徑等分來確定：圓圖中心|
|=0，最大圓周的|
|=1。有的圓圖在下面附有相應計算尺，其上標有反射係數、駐波係數，計算時可直接讀取。
3. 圓圖純電抗圓外面還有三個同心圓：最裡面一個圓標有以度表示的反射係數的相角
。另外兩個同心圓標出的是以波長
歸一化的傳輸線長度d/
（通常稱為電長度），分別表示向電源和向負載方向的電長度。
4. 為了避免圓圖上出現幾次零值點，電長度從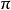
為起始點歸一化阻抗點z 所對應的電長度是由連線圓圖中心和z點的直線延長與電長度圓周的交點來確定，而不是由z 所在的電抗曲線與電長度圓周的交點來確定。
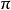
阻抗匹配
阻抗匹配（Impedancematching）是微波電子學裡的一部分，負載阻抗與激勵源內部阻抗互相適配，得到最大功率輸出的一種工作狀態,主要用於傳輸線上，來達至所有高頻的微波信號皆能傳至負載點的目的，不會有信號反射回來源點，從而提升能源效益。對於不同特性的電路，匹配條件是不一樣的。在純電阻電路中，當負載電阻等於激勵源內阻時，則輸出功率為最大，這種工作狀態稱為匹配，否則稱為失配。當激勵源內阻抗和負載阻抗含有電抗成份時，為使負載得到最大功率，負載阻抗與內阻必須滿足共軛關係，即電阻成份相等，電抗成份只數值相等而符號相反。這種匹配條件稱為共軛匹配。
匹配條件
①負載阻抗等於信源內阻抗，即它們的模與輻角分別相等，這時在負載阻抗上可以得到無失真的電壓傳輸。
②負載阻抗等於信源內阻抗的共軛值，即它們的模相等而輻角之和為零。這時在負載阻抗上可以得到最大功率。這種匹配條件稱為共軛匹配。如果信源內阻抗和負載阻抗均為純阻性，則兩種匹配條件是等同的。
方法
阻抗匹配大體上有兩種，一種是透過改變阻抗力（lumped-circuitmatching），另一種則是調整傳輸線的波長（transmission line matching）
改變阻抗力
把電容或電感與負載串聯起來，即可增加或減少負載的阻抗值，在圖表上的點會沿著代表實數電阻的圓圈走動。如果把電容或電感接地，首先圖表上的點會以圖中心旋轉180度，然後才沿電阻圈走動，再沿中心旋轉180度。重複以上方法直至電阻值變成1，即可直接把阻抗力變為零完成匹配。
調整傳輸線
由負載點至來源點加長傳輸線，在圖表上的圓點會沿著圖中心以順時針方向走動，直至走到電阻值為1的圓圈上，即可加電容或電感把阻抗力調整為零，完成匹配。
阻抗匹配則傳輸功率大，對於一個電源來講，當它的內阻等於負載時，輸出功率最大，此時阻抗匹配。最大功率傳輸定理，如果是高頻的話，就是無反射波。對於普通的寬頻放大器，輸出阻抗50Ω，功率傳輸電路中需要考慮阻抗匹配，可是如果信號波長遠遠大於電纜長度，即纜長可以忽略的話，就無須考慮阻抗匹配了。阻抗匹配是指在能量傳輸時，要求負載阻抗要和傳輸線的特徵阻抗相等，此時的傳輸不會產生反射，這表明所有能量都被負載吸收了。反之則在傳輸中有能量損失。高速PCB布線時，為了防止信號的反射，要求是線路的阻抗為50歐姆。這是個大約的數字，一般規定同軸電纜基帶50歐姆，頻帶75歐姆,對絞線則為100歐姆。
