可操作度

靈活性、可操作性的度量是機器人運動學方面的重要內容，可操作度是機器人靈活性的一個重要指標，一直是眾多學者的研究對象。可操作度的幾何意義為橢球各軸長的乘積，與其體積成正比。

Yoshikawa提出了以“可操作度橢球”的體積作為可操作度，可操作度對某一位形下機器人往各個方向運動的能力做出了綜合度量，可以用來衡量機器人的整體靈活性，作為設計和分析機器人的準則。

基本介紹

• 中文名：可操作度
• 外文名：Manipulability
• 實質：靈活性、可操作性的度量
• 最早提出：Yoshikawa
• 簡介：以可操作度橢球的體積為可操作度
• 套用學科：計算機科學、化學工程、機械工程

簡介

靈活性、可操作性的度量是機器人運動學方面的重要內容，一直是眾多學者的研究對象。Yoshikawa提出了以“可操作度橢球”的體積作為可操作度，並用該可操作度作為性能指標，對冗餘度機器人關節位形進行最佳化，實現了避關節奇異。其他學者從不同的角度提出了條件數、最小奇異值、最小條件數等靈活性的度量方法，並且將其套用於運動學控制。

可操作度的幾何意義為橢球各軸長的乘積，與其體積成正比。

可操作度對某一位形下機器人往各個方向運動的能力做出了綜合度量，可以用來衡量機器人的整體靈活性，作為設計和分析機器人的準則。

可操作度M(q)

機器人正向運動學由下式給出

式中：

p∈R^m×1為操作空間中機器人末端運動速度； 、

q˙∈R^n×1為關節運動速度；

J(q)∈R^m×n為Jacobian矩陣。對冗餘度機器人，m<n。

對於關節空間Rⁿ中的單位球

映射為笛卡兒空間R^m中的橢球

於是，定義可操作度M(q)為

若令

則

M(q)具有物理上的意義。

假設J的奇異值(SVD)分解為:

式中：U∈R^m×m，V∈R^n×n均為正交矩陣；

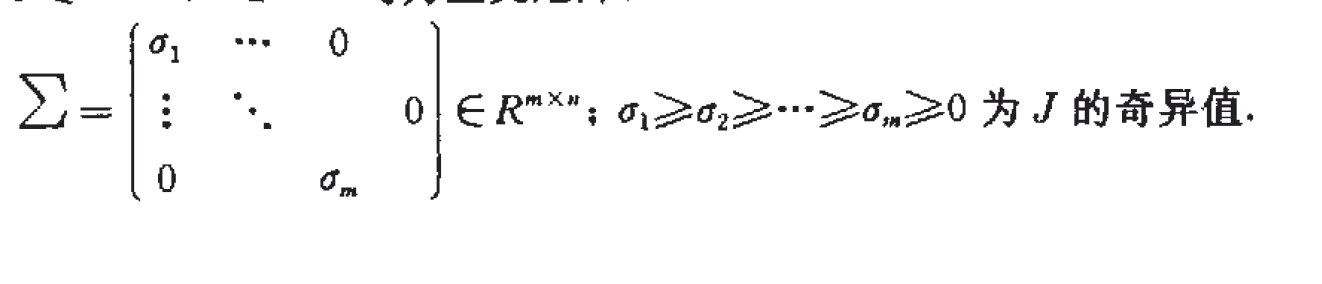
則

M(q)是主軸方向分別為U的列向量u₁，⋯u_m，一主軸長度分別為σ₁，⋯，σ_m的橢球的體積乘以一常數係數；σ₁，⋯，σ_m的大小表示在相應主軸方向上的運動能力。

M(q)綜合評價了機器人的各向靈活性，對機器人的靈活性和可操作性給予了整體的衡量。但是，以M(q)為目標函式進行運動學最佳化，追求靈活性的各向同性，實際上是追求可操作度橢球的體積最大，要求橢球面上的每一點都有足夠的長度。因此，當其套用於機器人控制時，存在著兩個方面的問題：

(1)正因為對M(q)的最佳化對各向同性提出了要求，也就是說，不必要地對非任務運動方向提出了和運動方向同樣的要求，浪費了部分最佳化能力。這一點，在多性能指標同時需要最佳化，最佳化空同不足時更顯突出；

(2)對於某一末端位置P，M(q)最優的可操作度橢球是唯一的。當機器人在某一關節位形，可操作度橢球的長軸與任務運動方向重合或很接近時，以M(q)為目標函式進行最佳化會對機器人該任務方向的運動能力起到減弱的作用。

方向可操作度

研究背景

由機器人關節的驅動器到機器人末端，可以看成是一個非線性的多輸入多輸出的傳動系統。運動靈活性反映了整個系統對運動的全局轉換能力。運動靈活性指標在機器人的設計、評價和運動規劃中起著重要的作用，各國學者對此展開了深入的研究。

絕大多數運動靈活性指標如條件數和可操作度都考慮了各個方向上的運動情況，稱為一般運動靈活性。而姚建初提出的方向可操作度是基於特定任務方向的，稱為特定運動靈活性。但這個指標有個最大的不足，就是它只考慮了機器人在某一特定方向上的運動轉換能力，忽略了其他方向上的運動能力。因此用該指標對冗餘度機器人進行軌跡規劃的時候，很有可能出現奇異或條件數較高的位形。

隨著機器人廣泛套用於航天、原子能工業等極限環境，對機器人的靈活性和可靠性提出了更高的要求。冗餘度機器人在無故障時刻時具有良好的靈活性；在發生故障時希望機器人仍然可以繼續完成作業。機器人的容錯控制保證系統更高的可靠性，並大大提高了其生存能力。

定義

方向可操作度在對機器人完成任務進行控制時，對特定任務而言，並不對機器人各個方向上的運動能力提出要求，我們所關心的是在任務要求的方向上機器人是否具有足夠的運動能力。因此，姚建初等提出了方向可操作度(Directional manipulability, DM)

式中， u 為沿末端運動速度方向的單位矢量，其物理意義很明確是沿著任務要求的特定方向上的運動轉換能力。而其幾何意義可以解釋為可操作度橢球沿著某一特定方向上軸長的平方，如圖所示。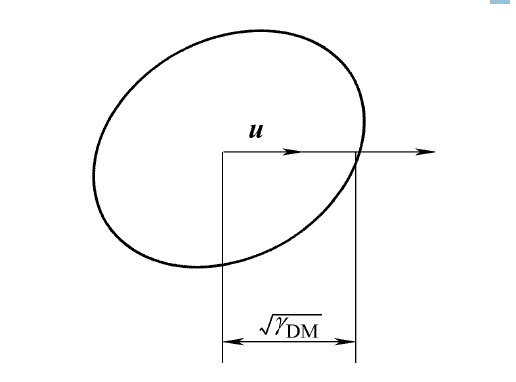

方向可操作度

缺點

基於條件數約束的方向可操作度DM 有效地表征了冗餘度機器人某一方向上的運動能力。對冗餘度機器人基於任務的方向可操作度的最佳化，可使位形更好地符合任務的要求，具有很好的實際套用意義。但是，該指標有個先天不足，就是該指標只考慮了某一特定方向上的運動能力，忽略了其他方向上的運動能力。因此，用該指標對冗餘度機器人進行運動規劃時，最佳化得到的可操作度橢球很可能只是在某一方向上的軸很長，而其短軸很短，這樣，在該位形下，條件數就會很大。在控制過程中，需要求解運動學逆解，條件數很大時，方程就處於病態，求解得到的結果誤差很大。因此，用DM 對冗餘度機器人進行運動規劃時的確能夠有效地增加任務方向上的運動能力，但有時這些位形對機器人的控制是非常不利的。

最佳化

對某一任務軌跡規劃後.可得到機器人末端的運動方向k₁，k₂，⋯.ki....如果對k₁，k₂，⋯.k_i....,用方向可操作度DM(q)作為目標函式進行最佳化，那么，基於任務的方向可操作度(TBDM，Task-Based Directional Manipulability measure)的最佳化描述成數學問題為：

目標函式：

約束條件：為機器人的正向運動學方程。