如果運算元半群{Tt|t≥0}滿足條件:當t>0時,對每個x∈X,向量值函式t→Ttx是強可微的,則稱{Tt|t≥0}為可微運算元半群。
基本介紹
- 中文名:可微運算元半群
- 外文名:semigroup of differentiable operator
- 適用範圍:數理科學
簡介,C0類運算元半群,向量值函式,定義式,參數方程,
簡介
可微運算元半群是具有某種可微性的C0類半群。
如果運算元半群{Tt|t≥0}滿足條件:當t>0時,對每個x∈X,向量值函式t→Ttx是強可微的,則稱{Tt|t≥0}為可微運算元半群。
C0類運算元半群
C0類運算元半群是一類具有強連續性的運算元半群。
設X是復的局部凸拓撲線性空間,L(X)表示X上的連續線性運算元全體。如果L(X)的運算元族{Tt|t≥0}滿足條件:
1、TsTt=Ts+t(s,t∈[0,+∞),T0=I);
2、(強)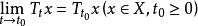 ;
;
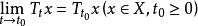
則稱{Tt|t≥0}為C0類運算元半群,簡稱C0類半群。
向量值函式
向量值函式是指分量都是關於同一自變數的一元函式,就是說 n 元向量值函式是x到xn上的映射。一個函式,若其值域是一個線性空間或一個線性空間的一個子集,則稱此函式為向量值函式。
定義式
r(t) ={f (t), g(t), h(t)}= f (t)i+ g(t)j+ h(t)k。
參數方程
Γ: x = f (t), y = g(t), z = h(t), t∈I。
