受控不變子空間

受控不變子空間（controlled invariant subspace）是控制理論的名詞。考慮一個以狀態空間表示的系統，其受控不變子空間為滿足以下條件的子空間：若系統一開始的初始狀態在此子空間內，有可能控制系統，讓系統始終在此子空間內。此概念是由Giuseppe Basile和Giovanni Marro所提出的（Basile & Marro 1969）。

基本介紹

• 中文名：受控不變子空間
• 外文名：controlled invariant subspace
• 分類：運算元理論、線性代數

定義

考慮用以下微分方程表示的線性系統

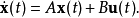
此處，x(t) ∈ 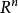表示系統的狀態，而u(t) ∈ 為輸入。矩陣A and B的大小分別是n × n和n × p。

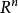
子空間V ⊂ 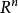是受控不變子空間，若針對任意x(0) ∈ V, ，都存在一輸入u(t)使得x(t) ∈ V，對所有非負的t都成立。

性質

子空間V⊂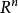是受控不變子空間，若且唯若AV⊂V+ ImB。若V受控不變子空間，則存在矩陣K使得輸入u(t) =Kx(t)，使狀態維持在V以內，這是簡單的回授控制.