反饋網路(Recurrent Network),又稱自聯想記憶網路,其目的是為了設計一個網路,儲存一組平衡點,使得當給網路一組初始值時,網路通過自行運行而最終收斂到這個設計的平衡點上。
基本介紹
- 中文名:反饋網路
- 外文名:Recurrent Network
- 定 義:網路通過自行運行而最終收斂
- 套用學科:自動化術語
- 縮寫:RN
- 工作方式:異步方式、同步方式
概念
定義
網路結構形式
 圖1
圖1 圖2
圖2工作原理
 圖3
圖3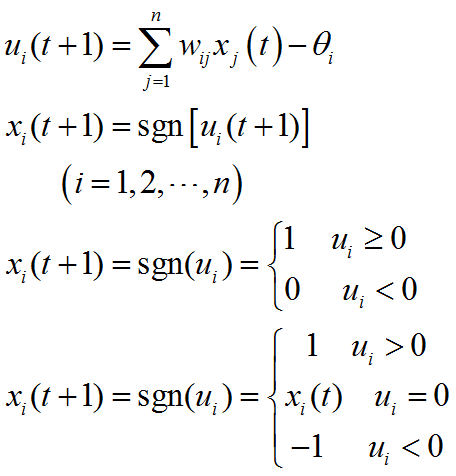 圖4
圖4 圖5
圖5 圖6
圖6 圖7
圖7 圖8
圖8
反饋網路(Recurrent Network),又稱自聯想記憶網路,其目的是為了設計一個網路,儲存一組平衡點,使得當給網路一組初始值時,網路通過自行運行而最終收斂到這個設計的平衡點上。
 圖1
圖1 圖2
圖2 圖3
圖3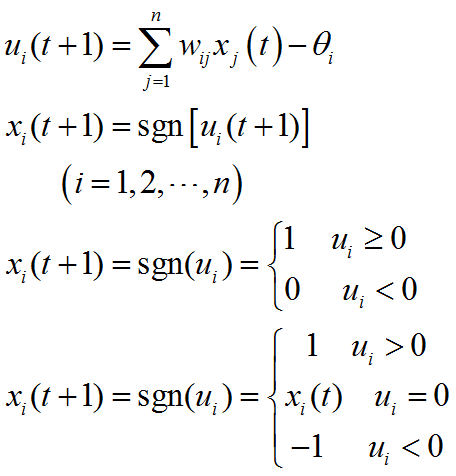 圖4
圖4 圖5
圖5 圖6
圖6 圖7
圖7 圖8
圖8反饋網路(Recurrent Network),又稱自聯想記憶網路,其目的是為了設計一個網路,儲存一組平衡點,使得當給網路一組初始值時,網路通過自行運行而最終收斂到這個設計的...
在社會心理學中,反饋是人際溝通過程中的一個重要環節。人際溝通過程,就是信息的交流過程,符合信息交流的過程。在人際溝通過程中,信息源通過一定信息渠道傳送出信息,...
反饋神經網路是一種將輸出經過一步時移再接入到輸入層的神經網路系統。...... 反饋神經網路是一種將輸出經過一步時移再接入到輸入層的神經網路系統。...
含有反饋網路的放大電路稱為反饋放大電路,反饋放大電路主要由基本放大電路和反饋電路兩部分組成。反饋可分為負反饋和正反饋。...
反饋電路是將放大器輸出信號(電壓或電流)的一部分或全部,回收到放大器輸入端與輸入信號進行比較(相加或相減),並用比較所得的有效輸入信號去控制輸出,這就是放大器...
反饋放大器,把輸出信號的一部或全部送回輸入端,以改變放大性能的放大電路。由輸出端送回輸入端的信號稱為反饋信號。...
網路式反饋結構是由專門機構行使反饋職能,反饋信息通過多渠道聯結的反饋結構。這種結構形式在社會管理系統中由四部分組成:(1)縱向網路,由垂直的各管理層次的辦事機構...
《網路分析和反饋放大器設計》是1945年在美國出版的一部作品,作者為H.W.博德。...... 《網路分析和反饋放大器設計》是1945年在美國出版的一部作品,作者為H.W....
外反饋是反饋方式的一種,外反饋是通過對行為結果的知悉而實現的反饋,而內反饋是通過內部刺激所提供的信息而實現的反饋。先外反饋後內反饋效果最好。外反饋也是串級...
所謂的正反饋效應就是某人做了符合他人價值觀,讓他人感到高興的、興奮的事情,並受到誇獎、鼓勵,進而做事人就會繼續努力的把這件事情做好,而且會越做越好。或者說,...
對於負反饋的增益Af=A/(1+AF),定義分母1+ A(s)B(s)=F(s)為反饋深度。反饋深度是一個十分重要的參數,表示引入反饋後放大電路的放大倍數與無反饋時相比所...
將輸出量的速度信號採用負反饋形式反饋到輸入端並與誤差信號比較,構成的迴路稱為速度反饋控制(velocity feedback control)。如果輸出量是機械角位移,可採用測速電機將...
最佳化反饋控制(Optimized feedback control)是指在給定的約束條件下用對象的狀態或者輸出來改造控制輸入,使得系統有期望的性能,尋求一個控制系統,使給定的被控系統性能...
電壓反饋(voltage feedback),簡稱VFB,套用在模擬電路中,是反饋的一種,若反饋量與輸出電壓成正比則為電壓反饋,與之對應的有電流反饋(CFB)。對於交流反饋,根據反饋...
反饋控制在現代電子工程中得到極為廣泛的套用。在廠、礦的工業生產中利用反饋挖制可實現生產自動化,在放大電路中利用反饋控制可以穩定靜態工作點和放大倍數,減少非...
反饋控制是指將系統的輸出信息返送到輸入端,與輸入信息進行比較,並利用二者的偏差進行控制的過程。實時控制利用數字電子計算機對事物連續變化過程的狀態及時收集,並按...
反饋系統結構是信息反饋系統內部的組織構成和關係。由於管理決策系統的體制不同,管理範圍和管理方式不同,反饋系統的結構呈現多種多樣的形式,主要有:串聯式單通道反饋...
延時反饋控制(Delayed feedback control)多以可程式線延時晶片和單片機為基礎,通過設計可程式延時控制系統,以達到對時間進行精密時延控制的需求。同時,作為大型複雜控制...
《教學反饋》是連載於晉江文學城的一本動漫同人類小說,作者是岳楓。...... 《教學反饋》是連載於晉江文學城的一本動漫...詞條標籤: 網路小說 , 文學作品 , 小說...
電流反饋(Circuit Feedback)英文縮寫CFB,在一個反饋電路中,若反饋量與輸出電流成正比則為電流反饋;若反饋量與輸出電壓成正比則為電壓反饋。通常可以採用負載短路法...
網路是由節點和連線構成,表示諸多對象及其相互聯繫。在數學上,網路是一種圖,一般認為專指加權圖。網路除了數學定義外,還有具體的物理含義,即網路是從某種相同類型的...
“反饋經濟”和移動網際網路、雲計算與大數據有關。它的特徵是能把移動設備獲知的各種數據時時的傳輸到雲中去,通過大數據池進行比較分析計算,反饋到你的手機終端或...
Ping是Windows、Unix和Linux系統下的一個命令。ping也屬於一個通信協定,是TCP/IP協定的一部分。利用“ping”命令可以檢查網路是否連通,可以很好地幫助我們分析和判定...
反饋體制是反饋系統內關係體系化、制度化的表現形式。反饋體制由目標、規範、組織三個部分構成。(1)目標是反饋系統運行的方向或目的。一般來說反饋系統的目標是尋找...
網際網路(英語:Internet),又稱網際網路,或音譯網際網路(Internet)、英特網,網際網路始於1969年美國的阿帕網。是網路與網路之間所串連成的龐大網路,這些網路以一組通用的...
