基本介紹
- 中文名:反幻方
- 性質:圖表
- 特徵:若干個排列整齊的數
- 優點:幾個數之和不相等
- 領域:數學
反幻方的定義,完美反幻方,n階反幻方與高階反幻方,反幻方的歷史來源:,
反幻方的定義
在一個由若干個排列整齊的數組成的正方形中,圖中任意一橫行、一縱行及對角線的幾個數之和不相等,具有這種性質的圖表,稱為“反幻方”。
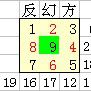
反幻方與正幻方最大的不同點是幻和不同,正幻方所有幻和都相同,而反幻方所有幻和都不同。所謂幻和就是幻方的任意行、列及對角線幾個數之和。如下圖3階反幻方的比較。
圖中框線外圍的數字之和就是幻和。紅色為偶數,黑色為奇數。
可以說反幻方是一種特殊的幻方。反幻方的幻和可以全部不同,也可以部分相同。如下圖多種3階反幻方。
3階反幻方如果旋轉、翻轉後的幻方算作同一個,總共有3120個3階反幻方,如果旋轉、翻轉後的幻方另外算一個,共24960個反幻方。
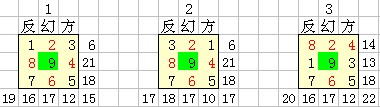 多種反幻方
多種反幻方完美反幻方
完美反幻方是指將連續的n^2個數字填到n*n的正方格中,使其中任意一行、任意一列、任意一條對角線上的 數字之和都不相等。並且各個方格內的自然數必須首尾相連,成為螺旋的形狀。當代美國科普作家加德納(M.Gardner,1914~)發 現,符合上述條件的反幻方只有兩個,它們是:
1 | 2 | 3 |
8 | 9 | 4 |
7 | 6 | 5 |
9 | 8 | 7 |
2 | 1 | 6 |
3 | 4 | 5 |
即一個轉進去的螺旋與一個轉出來的螺旋。
n階反幻方與高階反幻方
n階幻方是由前n^2(n的2次方)個自然數組成的一個n階方陣,其各行、各列及兩條對角線所含的n個數的和不相等。例子:
高次幻方是指,當組成幻方各數替換為其2,3,...,k次冪時,仍滿足反幻方條件者,稱此幻方為k次幻方。
反幻方的歷史來源:
幻方又稱為魔方,方陣或廳平方,它最早起源於我國。關於幻方的起源,我國有“河圖”和“洛書”之說。相傳在遠古時期,伏羲氏取得天下,把國家治理得井井有條,感動了上天,於是黃河中躍出一匹龍馬,背上馱著一張圖,作為禮物獻給他,這就是“河圖”,也是最早的幻方。伏羲氏憑藉著“河圖”而演繹出了八卦,後來大禹治洪水時,洛水中浮出一隻大烏龜,它的背上有圖有字,人們稱之為“洛書”。“洛書”所畫的圖中共有黑、白圓圈45個。把這些連在一起的小圓和數目表示出來,得到九個。這九個數就可以組成一個縱橫圖,人們把由九個數3行3列的幻方稱為3階幻方,除此之外,還有4階、5階...
4 | 9 | 2 |
3 | 5 | 7 |
8 | 1 | 6 |
後來,人們經過研究,得出計算任意階數幻方的各行、各列、各條對角線上所有數的和的公式為:
S=n(n ^2+1) /2
其中n為幻方的階數,所求的數為S.
三階幻方是最簡單的一種幻方,如果把經過旋轉和反射以後產生的幻方看作相同的幻方,那么,三階幻方只有一種構造方法。美國著名幻方大師馬丁·加德納發現:將1,2,3…9九個數隨意填進三階方陣中的九個格子裡,一般都會出現一些行或列或對角線上數字之和相等,於是他提出疑問:是否存在一個方陣,它的任一行,任一列或對角線上的數字之和都不相等呢?這就是反幻方問題,經過研究他終於找到了這種反幻方,有趣的是反幻方中的九個數竟形成了按順序咬接的“一條龍“。
1 | 2 | 3 |
8 | 9 | 4 |
7 | 6 | 5 |