由微觀粒子的全面性(或不可分辨性),全同粒子體系的波函式必是關於交換兩個粒子的全部變數為對稱的或反對稱的。並且這種對稱性不隨時間而改變。用對稱波函式所描述的全同粒子體系的量子態稱為對稱態。用反對稱波函式所描述的全同粒子體系的量子態稱為反對稱態。
基本介紹
- 中文名:反對稱態
- 外文名:antisymmetrical state
- 定義:反對稱波函式描述的量子態
- 套用學科:量子力學術語
- 範疇:理工科
- 涉及:波函式
概念,基本原理,
概念
由微觀粒子的全面性(或不可分辨性),全同粒子體系的波函式必是關於交換兩個粒子的全部變數為對稱的或反對稱的。並且這種對稱性不隨時間而改變。例如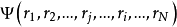 是表示
是表示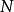 個全同粒子體系的波函式,其中
個全同粒子體系的波函式,其中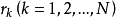 表示第
表示第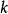 個粒子的全部變數。交換第
個粒子的全部變數。交換第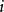 和第
和第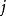 兩粒子的全部變數
兩粒子的全部變數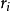 和
和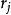 ,得一新的波函式
,得一新的波函式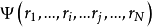 ,則必有
,則必有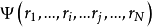 =
=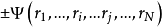 。取“+”、“—”分別代表
。取“+”、“—”分別代表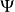 是對稱或反對稱波函式。用對稱波函式所描述的全同粒子體系的量子態稱為對稱態。用反對稱波函式所描述的全同粒子體系的量子態稱為反對稱態。
是對稱或反對稱波函式。用對稱波函式所描述的全同粒子體系的量子態稱為對稱態。用反對稱波函式所描述的全同粒子體系的量子態稱為反對稱態。
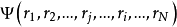
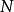
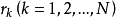
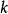
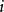
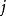
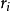
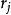
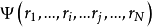
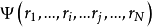
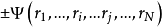
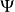
基本原理
全同粒子體系的量子力學理論,與經典理論對比具有許多新的特徵。量子力學研究的主要特徵是根據微觀客體的特殊物理性質,如熟知的粒子全同性原理或不可分辨性原理。
按照這個原理,體系的狀態在交換粒子的位置時仍然不變。我們來研究由兩個全同粒子所組成的體系的波函式的一般性質。體系的狀態由矢徑 ,三個空間量子數(
,三個空間量子數( ——主量子數,
——主量子數,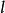 ——軌道量子數,
——軌道量子數,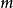 ——磁量子數。它們用簡單的符號
——磁量子數。它們用簡單的符號 來表示),以及自旋量子數
來表示),以及自旋量子數 來表示。按照通常所採用的符號,兩個粒子的波函式具有形式:
來表示。按照通常所採用的符號,兩個粒子的波函式具有形式:


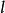
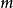


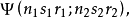
其次,我們引入粒子的置換算符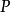 ,將它作用在波函式上歸結為或者變更坐標
,將它作用在波函式上歸結為或者變更坐標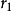 和
和 的位置,或者變更量子數
的位置,或者變更量子數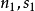 和
和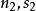 的位置:
的位置:
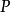
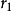

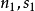
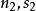
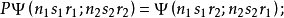
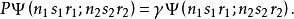
實際上,由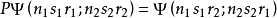 得出,兩次運用這個算符
得出,兩次運用這個算符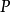 應該得到原來的狀態
應該得到原來的狀態
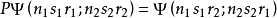
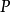
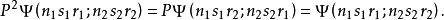
另一方面,從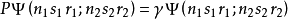 得出,
得出,
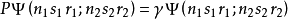
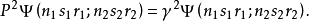
這樣一來,置換算符的本徵值等於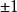 :
:
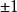
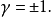
這個結果表示當交換粒子位置時,波函式或則保持不變: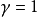 (這樣的函式稱為對稱的),或則變更符號:
(這樣的函式稱為對稱的),或則變更符號: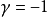 (這樣的函式稱為反對稱的)。
(這樣的函式稱為反對稱的)。
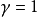
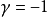
量子力學證實,全同粒子的集合可以處在只具有一定類型對稱性的狀態中。特別是,在自然界能實現的或則是對稱狀態(波函式是對稱的),或則是反對稱狀態(波函式是反對稱的),並且在這些狀態之間的量子躍遷是不可能的,不同類型對稱性的狀態取決於基本粒子本身的性質。

