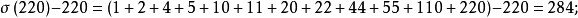友誼數也稱親和數、相親數、互滿數、互完數、友好數等，兩個自然數，一個數(除了該數自身以外)的所有(整數)因數的和，等於另一個數，則稱此兩數為一對友誼數。220與284為友誼數。因為220的整數因數為1、2、4、5、10、11、20、22、44、55、及110，其和是284；而284有整數因數1、2、4、71及142，其和是220。在106以下的數中，共有42對親和數。至今，人們已發現了近千對親和數。
基本介紹
- 中文名：友誼數
- 外文名：amicable[friendly] numbers
- 別稱：親和數、相親數、互滿數等
- 所屬學科：數學
- 相關概念：完全數等
- 提出者：畢達拉哥斯
- 相關人物：費馬，笛卡爾，歐拉等
基本介紹,相關介紹,友誼數的起源,
基本介紹
問題導引：
畢達拉哥斯把這樣的數對
稱為相親數，即友誼數：
的真因數之和為
，而
的真因數之和為
。最小的一對親和數是和。
介紹：
友誼數（也稱親和數）是一類著名的正整數，它與完滿數①有密切關係，如果正整數m的小於自身的因數之和等於n，而n的小於自身的因數之和又等於m，則稱m，n為一對親和數。即親和數是
和
同時成立的兩個數m，n。例如：
註：①在自然數中人們把恰好等於自身的全部真因子之和的數，定名為“完全數”，也叫“完滿數”。如：6=1+2+3；28=1+2+4+7+14就是兩個最小的完全數。
相關介紹
人們一般把親和數的發現歸功於古希臘的畢達哥拉斯(Pythagoras，約公元前572—前497年)學派。據說，當有人問畢達哥拉斯：“朋友是什麼?”他回答： “這是第二個自我，正如220與284。”但也有學者認為印度人和希伯來人在更早的時候已經知道親和數了。
親和數以其奇妙的性質， 在古代曾被蒙上相當神秘的色彩。例如認為分別寫上220與284的護符會使其佩帶者保持良好的友誼。希臘人用他們的字母表示數，因此每個人的名字也相應地可以表示一個數字。有一個未經證實的中世紀故事說： 有一位國王的名字在字數術上與284等價， 他因此要尋求一位名字代表220的女子做他的王后， 他相信這才是上天保證的美滿姻緣。
親和數非常稀少。自從古代發現了第一對後，直到1636年才由法國數學家費爾馬 (Fermat， 1601—1665)宣布17296和18416為另一對親和數。18世紀，歐拉(Euler.1707—1783，瑞士) 曾系統地尋找親和數，1747年給出一張30對的表，1750年擴展到60對以上。1866年，一個16歲的義大利男孩帕格尼尼(N.Paganini)發現了被人們忽視了的較小的一對1184和1210，成為親和數研究史上的一件奇事。現在，已經知道的親和數已有1000對以上。
有許多辦法尋求親和數對。阿拉伯數學家泰比特·伊本·柯拉(Tabit ibn Qorra，826—901)指出，對於
， 令
， 只要
全是素數，則
就是一對親和數。17世紀， 笛卡爾 (Descartes)重新得到這一公式。對n=2，它產生(220，284)，但它顯然只能產生較特殊的一類親和數。
現代，親和數對已被推廣為親和數鏈：鏈中每個數的因數之和等於下一個數， 而最後一數的因數之和等於第一個數， 如(12496， 14288， 15472，14536， 14264)。
1965年， 人們發現了一個以14316開頭的28環鏈。
數論中與親和數有關的許多問題， 既有趣， 又困難，例如，這種數是否有無限多對，就是一個至今尚未解決的著名難題。
友誼數的起源
友情真是有著無窮的號召力和影響力，它甚至超越了人和人之間的界限，連自然界中也有友情的存在。我們經常看見兩棵樹的根部緊緊相連，表現得親密無間，北燕南飛要成群結隊，團結友愛，共度艱難困苦。數學中也有友情，某些數字之間有著某種特殊的、天然的親和，人們將這些數字叫做親和數。
所謂親和數是指具有這樣關係的兩個數字，每個數的真因子之和都恰好等於另一個數。親和數和人們是老朋友了，很久以前人們就發現了它們。世界上第一對被人們發現的親和數是220和284，它最早出現在公元4世紀，哲學家亞姆利康的書中，首次記載了這對數。而親和數這個概念是在公元前5世紀的時候才開始被人們使用的，是古希臘數學家畢達哥拉斯最先引用的。
古希臘數學家畢達哥拉斯在研究中發現，220的所有真因數1、2、4、5、10、11、20、22、44、55、110，其和是284；而284的所有真因數1、2、 4、71、142，其和又恰是220。它們之間的這種特殊的關係只是一種巧合嗎?還是只是小荷才露尖尖角呢?
“數為物源”，畢達哥拉斯對此深信不疑，這也是畢達哥拉斯學派的信條。但是有一位他的學生對“數為物源”提出了質疑，這一信條是否就是真理呢?於是他就向畢達哥拉斯提出了疑問：“既然說‘數為物源’，那么世界上所有的事就都是數字決定的嗎?那我結交朋友時，數字又起了什麼作用呢?”畢達哥拉斯作出了近乎完美的回答，捍衛了他一生所深信不疑的信條，他回答說：“朋友是你靈魂的倩影，就像220和284一樣親密。”這就是有關親和數名稱的由來。後來，畢氏學派宣傳說：人之間講友誼，數之間也有“相親相愛”，就是出於這個典故。
可惜畢達哥拉斯並沒有如願以償地發現第二對親和數。兩千年以後，法國的費馬和笛卡兒發現了第二對親和數17296和18416。在這期間，無數的數學家為了尋找出第二對親和數苦思勞心，從沒停止過對第二對親和數的尋找。數海無邊，要找出親和數談何容易，有些數學家甚至窮其一生，但是都沒有獲得結果。
由於對親和數的尋找始終沒有結果，人們開始懷疑是不是在自然數中只存在那一對親和數，有些人捕風捉影，甚至給親和數帶上了迷信的帽子。好在費馬和笛卡兒及時地發現了第二對親和數，捍衛了科學的嚴肅性，在親和數發現的歷程上劃破了沉寂的夜空。笛卡兒和費馬憑藉他們天生對數字的敏感和堅持不懈的努力，在短短的兩年內就得出了第二對親和數。人們又重新燃起了希望，後來的數學家歐拉一下就給出了三十對親和數。
目前，人們還沒有找到能夠普遍尋找到親和數的公式。計算機的問世使尋找親和數變得簡單明了了，但是，即使是計算機也沒有突破長久以來的局限，在未來的漫長旅途中我們的數學家會不會給我們帶來驚喜呢?讓我們拭目以待吧!
