參考系拖拽

愛因斯坦的廣義相對論預言了處於轉動狀態的質量會對其周圍的時空產生拖拽的現象，這種現象被稱作參考系拖拽（英文：Frame-dragging）或慣性系拖拽（英文：Inertial frame dragging）。因轉動而產生的參考系拖拽的相應理論最早由奧地利物理學家約瑟夫·冷澤與漢斯·提爾苓於1918年通過廣義相對論推導出，因此參考系拖拽也常常被叫做冷澤-提爾苓效應（英語：Lense-Thirring Effect）。

基本介紹

• 中文名：參考系拖拽
• 外文名：Frame dragging
• 別稱：慣性系拖拽

簡介

冷澤與提爾苓預言物體的轉動會導致其周圍時空參考系的改變，從而使周圍物體的位置和牛頓力學下的經典結果產生偏差。不過理論預言這種偏差將非常之小，大約只有幾萬億分之一。想要在實驗中觀測到這種現象，需要對大質量的旋轉物體（例如行星或恆星）使用高靈敏度的儀器進行探測，例如圍繞地球公轉的人造衛星軌道會因地球自轉而產生細微的變化。更一般的，這種由加速質量而產生的引力場變化可以歸結到引力磁學的研究領域。

參考系拖拽的分類

轉動的參考系拖拽:冷澤-提爾苓效應

廣義相對論和引力磁學等有關替代理論都預言處於轉動的大質量物體周圍會產生參考系的拖拽。根據冷澤-提爾苓效應，一個處於遠處的觀察者將看到圍繞中心物體轉動的參考系內的時鐘走得最快；這也說明在觀察者看來，與物體轉動速度方向相同的光將比與轉動速度方向相反的光走得更快。冷澤-提爾苓效應是最著名的廣義相對論效應之一，這要部分歸功於引力探測器B的實驗觀測。

直線的參考系拖拽

類似於轉動產生的參考系拖拽，移動也會產生類似的效應。儘管這種效應是否和轉動的效應一樣在理論上成立有著爭議，但實驗驗證的高度困難導致其相關討論比轉動效應少得多，也常常在討論參考系拖拽的文章中被忽略，不過愛因斯坦在其1921年的著作《相對論的意義》中敘述了這種效應。

靜止質量的增加

這是愛因斯坦在同一著作中提到的第三種效應：當周圍有質量存在時，一個物體的慣性會增加。儘管嚴格說這不是一種參考系的拖拽（而愛因斯坦在論文中並未使用參考系拖拽一詞來概括這幾種效應），愛因斯坦在廣義相對論下使用了與以上兩種參考系拖拽效應相同的推導過程得到了這種效應。同樣，這也是一種非常微小的效應，在實驗中難以觀測。

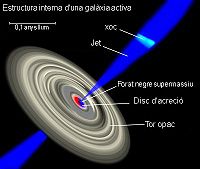相對論性噴流——在一個活動星系核的周圍

參考系拖拽的實驗驗證

1976年范·帕騰（Van Patten）和伊夫利特（Everitt）在他們的論文中提出了一個專門用於觀測冷澤-提爾苓效應的實驗構想：測量一對置於地球極軌道上的相向繞轉的太空飛行器的節點的冷澤-提爾苓進動，而太空飛行器上的測量儀器需要滿足無拖拽條件。1986年，丘弗里尼（Ciufolini）提出了一個基本等效但更廉價的版本，他提議發射一枚被動的沿測地軌道運行的衛星，其軌道和1976年發射的LAGEOS衛星的軌道相比除了軌道平面相差180度外完全相同，這枚衛星和LAGEOS的共同構造被稱作蝴蝶式配置。在這種情況下，系統的可觀測量為LAGEOS衛星和這枚新衛星（其後在不同場合下被稱作為LAGEOS III、LARES或WEBER-SAT）的節點總數。儘管這種構想被很多研究小組進行過詳細的研究，還沒有將這個構想付諸實踐。原則上，在蝴蝶式配置下人們不僅可以測量節點的總數，還能夠觀測到近地點之間相差的距離，雖說在實際運行中系統的克卜勒軌道參數受到的來自非引力的微擾影響會更大，例如來自太陽的輻射壓。這也是在實際運行中需要實現動態的無拖拽技術的原因。其他被提出的構想包括發射一顆處於近極軌道且較低高度的衛星，但這種構想已經被證明不可行。近年來為了提高實際架設蝴蝶式配置的可能性，有人提出LARES/WEBER-SAT衛星將有能力驗證由Dvali、Gabadaze和Porrati建立的多維膜世界模型，並能夠將現今對等效原理驗證的精確度提高兩個數量級，不過這種說法已經被證明非常不現實。

我們只局限於討論有關已發射衛星的研究的情形，最早提出利用LAGEOS衛星以及衛星雷射測距（SLR）技術來測量冷澤-提爾苓效應的構想可追溯至1977-1978年。而真正有效的實驗測試則是在1996年通過LAGEOS和LAGEOS II完成的，實驗中採用了對兩枚衛星的節點和LAGEOS II的近地點位置的恰當組合。最近的一次來自LAGEOS衛星的探測是在2004-2006年，觀測中沒有使用LAGEOS II的近地點，而只採用了對兩架太空飛行器節點觀測結果的線性組合。實驗結果和廣義相對論的預言並不矛盾，然而計算得到的觀測總誤差卻引發了一些爭論。另一個在火星引力場中觀測冷澤-提爾苓效應的測試結果是根據對火星全球探勘者號（MGS）的位置數據進行恰當分析後得到的，不過這個結果也引發了爭議。此外還有觀測太陽自轉對太陽系內行星軌道產生的冷澤-提爾苓效應的嘗試，廣義相對論對冷澤-提爾苓進動的預言和觀測到的行星近日點進動的修正相符合，但誤差依然比較大；以及對環繞木星的伽利略衛星的觀測，這同時也是最初由冷澤和提爾苓提出的實驗建議。

引力探測器B正在對另一種引力磁學的效應即希夫進動進行實驗觀測，並期望達到1%或更好的誤差。然而這個目標還是個奢望，2007年4月的最初結果表明能達到的誤差範圍在256-128%之間，並期望在2007年12月時能夠縮小至13%。2005年物理學家艾奧里奧（Iorio）指出，如要在地球引力場中觀測冷澤-提爾苓效應達到1%的誤差水平，還需要發射至少兩個新的衛星，並且最好能夠採用偏心率很高的軌道以及一些能夠抵消非引力微擾的動態機制。最近，義大利航天局（ASI）宣布將於2008年底使用VEGA運載火箭發射LARES衛星[1]，其目標是將地球引力場中冷澤-提爾苓效應的測量達到1%的誤差精度，但有人對這一計畫能否成功表示懷疑。近來還有墨菲等人報告了一個通過月球雷射測距對引力磁性的間接觀測實驗，並聲稱其誤差小於0.1%；但物理學家科佩金（Kopeikin）對月球雷射測距技術能否感應到引力磁性的存在表示疑問。

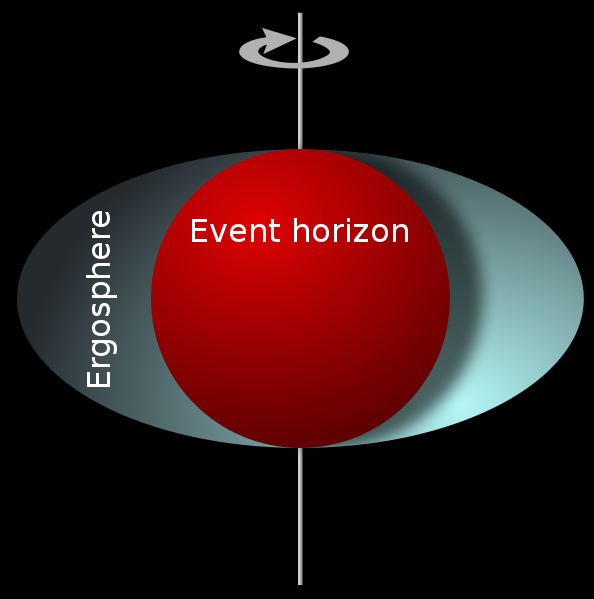
克爾度規在兩個表面上具有奇性

天體物理學的證據

相對論性噴流或許可以為參考系拖拽的存在提供直接證據：在一個旋轉黑洞的能層內由冷澤-提爾苓效應產生的引力磁力和由羅傑·彭羅斯爵士提出的能量抽取機制一起可以被用來解釋對相對論性噴流觀測到的性質。由雷瓦·凱·威廉士發展的引力磁學模型預言了已被觀測到的由類星體和活動星系核發射的高能粒子（～吉電子伏特）、X射線和伽瑪射線的光子抽取、平行於極軸的相對論性噴流以及噴流相對於軌道平面的非對稱結構等現象的存在。

參考系拖拽的數學推導

描述參考系拖拽的最直接方法是使用克爾度規，克爾度規描述了一個質量為M，具有角動量J的旋轉黑洞周圍的時空幾何。

這裡r_s是史瓦西半徑。

度規中其他變數的意義為

在非相對論極限下，當質量M(或等效地，r_s)趨於零時，克爾度規成為扁球面坐標系下的正交度規形式：

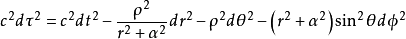
我們可以將它重新寫作如下形式

這個度規和一個以角速度Ω旋轉的坐標系等價，其中角速度Ω和半徑r及余緯θ有關：

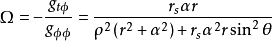
在赤道面上可以簡化為：

從而我們看到，一個處於旋轉狀態的中心質量能夠導致周圍慣性參考系的轉動，這就是參考系拖拽。

克爾度規在兩個表面上具有奇性，內表面是球形的事件視界，外表面是一個扁球面。黑洞的能層處於這兩個表面包圍的時空中，在能層內度規的純時間分量是負值，這意味著它是類空的。其結果是處於其中的粒子需要和中心質量共同旋轉才能保持類時的性質。

一個旋轉黑洞的能層內的參考系拖拽效應是一個極端的版本。從數學形式上看，克爾度規存在有兩個奇性的面，內表面對應著一個和史瓦西度規類似的球面視界：

• {\displaystyle r_{inner}={\frac {r_{s}+{\sqrt {r_{s}^{2}-4\alpha ^{2}}}}{2}}}
  

在這個半徑上度規的純徑向分量g_rr趨於無窮大。

奇性的外表面不是一個球面，而是一個扁球面。這個扁球面在其旋轉軸的極點處和內表面相重合，這時的余緯度θ等於0或π；而其半徑由下式給出：

• {\displaystyle r_{outer}={\frac {r_{s}+{\sqrt {r_{s}^{2}-4\alpha ^{2}\cos ^{2}\theta }}}{2}}}
  

在這個半徑上度規的純時間分量g_tt由正變為負，內外奇性表面所包圍的空間被稱作能層。一般來說，沿世界線運動的運動粒子所經歷的固有時總是正的，但在時間分量g_tt為負的能層中這無法做到，除非這個粒子同時也以不低於Ω的角速度圍繞中心質量M旋轉。當然，參考系拖拽效應發生在任何旋轉質量周圍的任何位置，而不僅僅在能層中。

參考系拖拽力的公式

根據Lev Laudau The classic theory of fields

• {\displaystyle F={\frac {SJj}{r^{4}}}}
  

J為中心質量自旋角動量 j為周圍質量公轉角動量 S為史氏常數

• {\displaystyle S={\frac {2G}{c^{2}}}}
  

而旋轉參考系拖拽能量公式為

• {\displaystyle E={\frac {SJj}{r^{3}}}}