卡爾馬-沃爾什定理

卡爾馬-沃爾什定理（Kalmar-Walsh theorem）是關於插值多項式收斂性的定理。

基本介紹

• 中文名：卡爾馬-沃爾什定理
• 外文名：Kalmar-Walsh theorem
• 適用範圍：數理科學

簡介

卡爾馬-沃爾什定理是關於插值多項式收斂性的定理。

設K是複平面上的一個緊子集，其餘集是一個單連通區域，f(z)是K上的解析函式， ，L_n(f,z)是在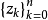 上插值f(z)的拉格朗日插值多項式。卡爾馬-沃爾什定理斷言：要使對任何在K上解析的函式f(z)，極限

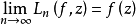在K上一致成立的充分必要條件是節點陣 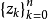在K上是一致分布的。

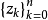
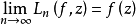
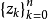
解析函式

解析函式是區域上處處可微分的複函數。17世紀，L.歐拉和J.leR.達朗貝爾在研究水力學時已發現平面不可壓縮流體的無旋場的勢函式Φ(x,y)與流函式Ψ(x,y)有連續的偏導數，且滿足微分方程組，並指出f(z)=Φ(x,y)+iΨ(x,y)是可微函式，這一命題的逆命題也成立。

柯西把區域上處處可微的複函數稱為單演函式，後人又把它們稱為全純函式、解析函式。B.黎曼從這一定義出發對複函數的微分作了深入的研究，後來，就把上述的偏微分方程組稱為柯西-黎曼方程，或柯西-黎曼條件。

收斂性

收斂性是數學分析的基本概念之一，它與“有確定的（或有限的）極限”同義，“收斂於……”相當於說“極限是……（確定的點或有限的數）”。

在一些一般性敘述中，收斂和收斂性這兩個詞(在外語中通常是同一個詞)有時泛指函式或數列是否有極限的性質，或者按哪一種意義(什麼極限過程)有極限。在這個意義下，數學分析中所討論的收斂性的不同意義(不同類型的極限過程)大致有：對數列(點列)只討論當其項序號趨於無窮的收斂性；對一元和多元函式最基本的有自變數趨於定值(定點)的和自變數趨於無窮的這兩類收斂性；對多元函式還有沿特殊路徑的和累次極限意義下的收斂性；對函式列(級數)有逐點收斂和一致收斂。