半分離解是概周期微分方程的一個概念。
半分離解(semi-separated solution.概周期微分方程的解抓t>CK稱為在K中是半分離的,如果對tER+,整個都包含在K中的任何解側t),都存在常數a<卯}0,使得}」抓t>一扛t) }} } aC卯(tER>.這個概念是芬克(Fink,A. M.)於1972年引進的.
設.f(t,x>是u. a. p.的,對二EK,微分方程
在K中的解抓t)所具有的性質P稱為半分離的,如果對方程在K中具有性質P的任一其他的解}G(t>,都存在常數.1(}O,婦}0,使得}!抓t)一粼t)日)1(5o,婦(t E[一二,0習>. a(}o,}G)稱為可分離常數.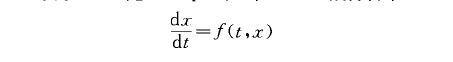
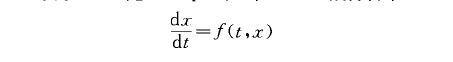
如果半分離性質P是可繼承的,且方程dx/dt=.f <c,二)在K中僅有有限個具有性質P的解,那么對每一gEH(f),方程dx/dt=g (t, x)在K中有相同個數具有性質屍的解,且可選取可分離常數,與解和方程無關.半分離性質的可繼承性對保證概周期解的存在性起著重要作用.如果一致概周期微分方程僅有有限個在K內具有性質屍的解,又性質屍是半分離和可繼承的,那么,每個這樣的解在R一上是漸近概周期的,從而在K內有概周期解.
