勾股求弦作圖

我國古代，把直角三角形的兩條直角邊叫做勾和股，斜邊叫做弦。勾股求弦作圖(construction of seeking hypotenuse chord of given legs of a triangle)即已知直角三角形的直角邊求做斜邊。

基本介紹

• 中文名：勾股求弦作圖
• 外文名：construction of seeking hypotenuse chord of given legs of a triangle 
• 所屬學科：數學（平面幾何）
• 簡介：已知直角三角形的直角邊求做斜邊

基本介紹

“勾股求弦”作圖即：作一線段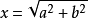，其中都是一已知線段。

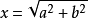
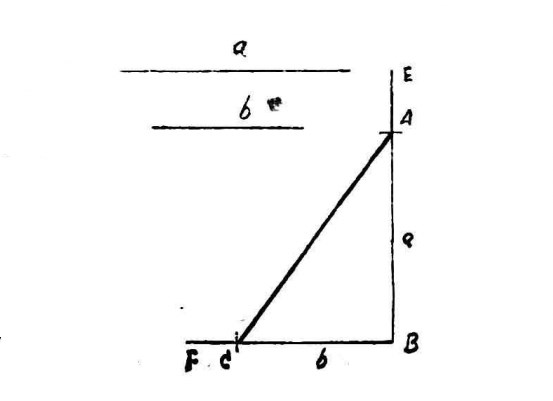
已知 線段a、b

求作 線段x使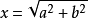

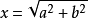
作法 作一直角∠EBF，在BE上截取BA=a，在BF上截BC=b，連AC，則AC即為所求x。

圖1

相關歷史介紹

《周髀算經》 我國古代，把直角三角形的兩條直角邊叫做勾和股，斜邊叫做弦。在數學古書《周髀算經》中，曾記載了周公和商高的一段問答，其中談到“故折矩，以為勾廣三，股修四，徑隅五”。“勾廣”就是勾長，“股修”就是股長，“徑隅”就是弦長。這句話的意思是說，如果將一根直尺折成一個直角，若短直角邊的長為3，長直角邊的長為4，那么斜邊的長一定為5。在《周髀算經》中記載的榮方和陳子的問答中，談到了由勾股求弦的一般方法“勾股各自乘，並而開方除之”。可見古代勞動人民已將勾股定理運用於生產實踐之中。一般認為《周髀算經》成書於公元前1世紀，可見我國至少在2100年前就發現了勾股定理。

《勾股舉隅》《勾股舉隅》為梅文鼎研究中國傳統勾股算術的著作，全書一卷，其中的主要成就，是對勾股定理的證明和對勾股算術算法的推廣。書中首列“和較名義”，其次以兩幅“弦實兼勾實股實圖”來說明勾股定理(如下圖)，其論說的根據是出入相補原理。

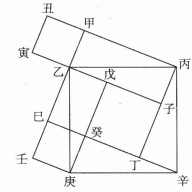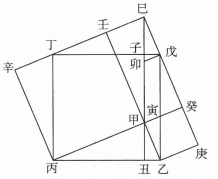圖2

圖2

在問題的陳述上，本書以“問題”、“法”、“論曰”為主，法為算法，論曰為證明，若有另外的算法，則再加，上“又法”及“論日”，部分題目則給出了“又簡法”，即速算法。書中的每個問題皆附上圖形，圖形的目地主要是用來說明出入相補法。在內容上，本書大致上可分作兩部分，一為勾股算術，另一主要為勾股測量。前者共列13題，後者則為6問。前者內容如下：

編號	題名	已知條件(a為勾，b為股，c為斜邊)
1	勾股求弦	a，b
2	勾弦求股	ab/2，c
3	勾股積與弦求勾股	ab/2，b+a
4	勾股積與勾股和求勾股	ab/2, c-(b-a)
5	勾股積與弦較較求諸數	ab/2，c+(b- a)
6	勾股積與弦較和求諸數	ab/2，(b-a)-c
7	勾股積與弦和較求諸數	ab/2，(b-a)-c
8	勾股積與弦和和求諸數	ab/2，c+(b+a)
9	勾弦和股弦和求諸數	c+a, c+b
10	勾弦較股弦較求諸數	c-a，c-b
11	勾股較弦和和求諸數	b-a，c+(b+a)
12	勾股較弦和較求諸數	b-a，(b+a)-c
13	弦與勾股和求勾股用量法	c，b+a

其中“勾股積與弦較較求諸數”(5)、“勾股積與弦較和求諸數”(6)、“勾股積與弦和較求諸數”(7)、“勾股積與弦和和求諸數”(8)、“勾股較弦和和求諸數”(11)、“勾股較、弦和較求諸數”等六個問題在歷史上是首度出現。此外，梅文鼎對這些題目中所給的算式中，最重要的是:

[c-(b-a)][c+(b+a)]=[(b+a)-c][(b+a)+c]=4(ab/2).

梅文鼎對其評價很高，他認為此式“乃立之根也。而其理皆具古圖中，學者所宜深玩”。這裡的“古圖”指的即是趙爽注《周髀算經中》之“勾股圓方圖”，對此式的證明也是利用此圖來完成的。值得注意的是，“弦與勾股和求勾股用量法”一題中所用的標尺作圖之方法，與徐光啟《勾股義》中“勾股求容圓”來作比較，可以發現梅文鼎在標尺作圖的概念已相當正確，顯示梅文鼎對《幾何原本》有一定深度的了解。另外，從梅文鼎在測量問題上所使用的出入相補法來看，其內容相當貼近楊輝乃至於劉徽的作法，有別於明末西方傳人的測量方法。