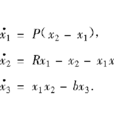1963年，Lorenz發現了第一個混沌吸引子——Lorenz系統，從此揭開了混沌研究的序幕，該系統也稱為Lorenz混沌系統。從此，人們不斷發現新的混沌奇異性，不斷地加深與統一對混沌的理解。
基本介紹
- 中文名：勞倫茲混沌系統
- 外文名：Lorenz chaotic system
- 別稱：Lorenz混沌系統
- 學科：控制科學與工程
- 提出者：Lorenz
- 時間：1963年
基本概念,模型,參數辨識,關係區別,
基本概念
1963年，Lorenz發現了第一個混沌吸引子——Lorenz系統，從此揭開了混沌研究的序幕。人們不斷發現新的混沌奇異性，不斷地加深與統一對混沌的理解。混沌系統是指在一個確定性系統中，存在著貌似隨機的不規則運動，其行為表現為不確定性、不可重複、不可預測，這就是混沌現象。混沌是非線性動力系統的固有特性，是非線性系統普遍存在的現象。
模型
Lorenz系統是數值試驗中最早發現的呈現混沌運動的耗散系統，其狀態方程為：
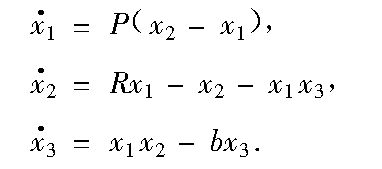
在a=10，b=8/3，c=28時呈現混沌態。該系統的一個簡單物理實現是流體在下方加熱上方冷卻的熱對流管中的環流，此時，x1是流體速度，x2和x3分別為水平和垂直的溫度差，P與流體的Prandtl數成比例，b是與空間相關的常數，R與流體的Rayleigh數成比例。
參數辨識
自從1963年以來，對著名Lorenz系統的混沌行為已有系統研究隨著混沌控制問題引起人們注意，控制Lorenz系統的混沌也有一系列工作。然而現有的工作，大多數控制方法均是在系統參數已知的情況下給出的；對於系統中存在未知參數時的情況較少被涉及。現存的很多控制方法，在參數未知的情況下不再適用。系統中未知參數的存在，為系統控制方法的設計增加了難度。
下面是一種辨識系統局部參數的方法，其特點是：將未知參數作為系統的未知狀態來處理，從而將辨識參數問題轉化為未知狀態的觀測辨識問題。通過狀態觀測器的設計，來解決系統參數的辨識問題。
當系統參數P，R為已知參數，而b為未知參數時，在實際中需要得到未知參數b的值。然而，在很多情況下，未知參數的動態信息很難被得知，因此假定
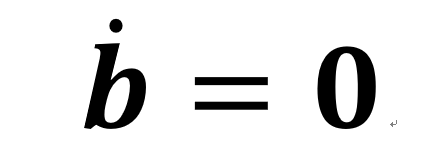
對於未知的參數b，把它作為狀態變數，則可得到一增廣的系統狀態變數
更進一步，假設系統式中的所有狀態均可得到，只需辨識未知的參數。
給出如下觀測器：
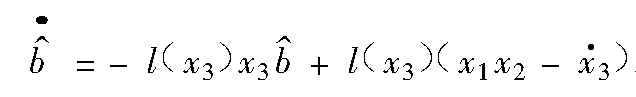
定義一個輔助變數
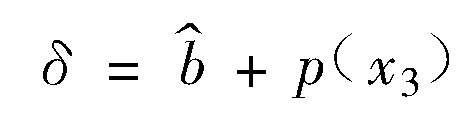
且令
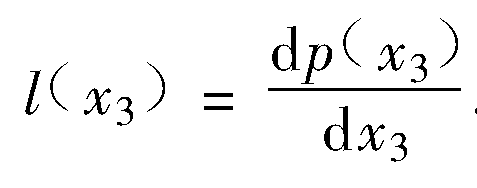
綜合上面方程得到：
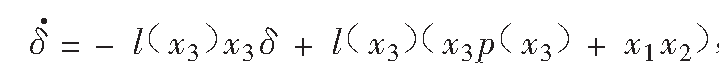
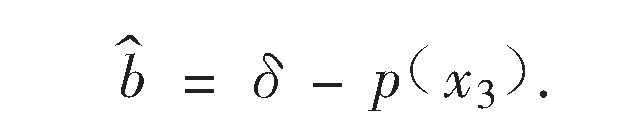
稱上面兩式組成的觀測器為未知參數辨識觀測器，其中p(x3)為被設計的函式。
動力系統辨識問題是動力學研究的逆問題，它利用系統在試驗和運行中測得的輸入輸出數據，採用系統辨識技術，建立反映系統本質特性的數學模型，並辨識出模型中的待定參數。一般情況下，系統的動力學方程是已知的，需要辨識的只是動力學方程中的某些待定參數，諸如系統的模態參數或剛度，阻尼等結構物理參數，這屬於典型的“灰箱問題”。
關係區別
Lorenz系統和陳氏混沌系統
1999年，美國休斯頓大學陳關榮教授發現了一個新的混沌吸引子——Chen系統，即陳氏混沌系統，它與Lorenz系統類似，但不拓撲等價而且更複雜。
Lorenz系統和陳氏混沌系統分別屬於兩個相反的類：
Lorenz系統滿足
，而陳氏混沌系統卻滿足
，在這種意義下，他們是對偶的兩個動力系統。由於陳氏混沌系統比Lorenz系統具有更複雜的拓撲結構和動力學行為，這一方面使得它在信息加密和保密通信等領域有著更廣闊的套用前景，另一方面使得陳氏混沌系統很難控制，許多對Lorenz系統輕而易舉的控制方法對陳氏混沌系統卻不太理想甚至無效。儘管如此，目前對該系統的控制已有不少有效的控制方法，如：逆最優控制、識別控制、數字控制、模糊控制、脈衝控制、自適應控制等，隨著研究的不斷深入，在實際套用中必然要追求實施控制的有效性、代價大小和難易程度。
