法國數學家。1906年11月7日生於法國南特,1926~1929年就讀於巴黎高等師範學校。1933年在巴黎大學獲科學博士學位。1947~1978年任法蘭西學院的微分和泛函方程教授。基於他把拓撲方法用於研究微分方程方面的先驅性工作,1979年獲沃爾夫獎。早在1934年他就在“擬導數”的名稱下系統地引進了 的廣義微分運算元;以及給出局部可積函式正則化的過程。1934年他和J.P.紹德爾合作給出勒雷-紹德爾不動點定理,這是當時代數拓撲在泛函方程求解中富有成果的套用,至今仍是研究非線性微分方程解的存在性的有力工具。他和其他人一起開創了對粘性可壓縮流體的納維-斯托克斯方程組的邊值問題的解的存在性和解的性質的研究。他在40年代開創了譜序列理論和層理論的研究,這兩種理論現在已成為許多數學分支中的重要的基本工具。勒雷對雙曲型偏微分方程組和拉格朗日分析等方面有重要貢獻。他是法蘭西研究院的院士,也是美國科學院和蘇聯科學院以及另外一些國家的科學院的國外院士。
人物生平,主要成就,
人物生平
法國數學家。1906年11月7日生於法國南特,1926~1929年就讀於巴黎高等師範學校。1933年在巴黎大學獲科學博士學位。1947~1978年任法蘭西學院的微分和泛函方程教授。基於他把拓撲方法用於研究微分方程方面的先驅性工作,1979年獲沃爾夫獎。早在1934年他就在“擬導數”的名稱下系統地引進了的廣義微分運算元;以及給出局部可積函式正則化的過程。1934年他和J.P.紹德爾合作給出勒雷-紹德爾不動點定理,這是當時代數拓撲在泛函方程求解中富有成果的套用,至今仍是研究非線性微分方程解的存在性的有力工具。他和其他人一起開創了對粘性可壓縮流體的納維-斯托克斯方程組的邊值問題的解的存在性和解的性質的研究。他在40年代開創了譜序列理論和層理論的研究,這兩種理論現在已成為許多數學分支中的重要的基本工具。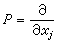 勒雷,J.
勒雷,J.
 勒雷,J.
勒雷,J.主要成就
勒雷對雙曲型偏微分方程組和拉格朗日分析等方面有重要貢獻。他是法蘭西研究院的院士,也是美國科學院和蘇聯科學院以及另外一些國家的科學院的國外院士。
