勒穆瓦納線

勒穆瓦納線(Lemoine line)是一個共線點問題。過三角形的頂點所作外接圓的切線分別與對邊(所在直線)的交點共線，這直線叫做三角形的勒穆瓦納線。

基本介紹

• 中文名：勒穆瓦納線
• 外文名：Lemoine line
• 所屬學科：數學
• 所屬問題：平面幾何（三角形）
• 提出者：Lemoine
• 簡介：一個共線點問題
• 別名：Lemoine線

基本介紹

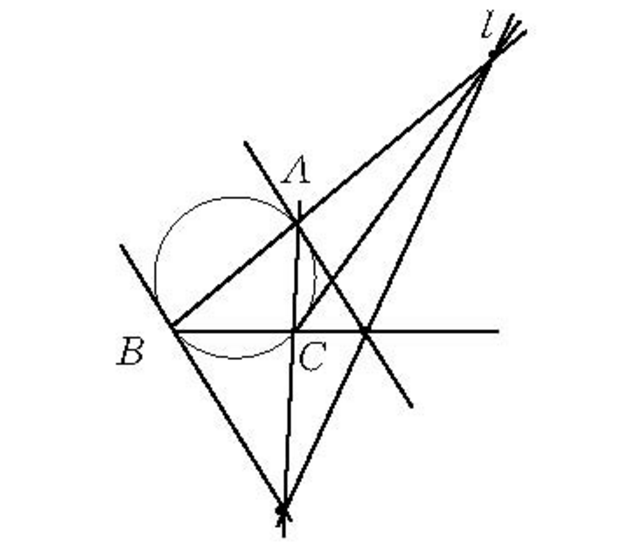
過三角形的頂點所作外接圓的切線各與對邊所在直線的交點在一直線上(如圖1所示)，這條直線稱為勒穆瓦納線(Lemoine line)。

此結論是由Lemoine首先發現的，所以這樣的直線被命名為三角形的Lemoine線。

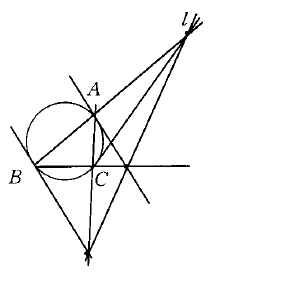
圖1

命題的證明

先介紹一個定理——梅內勞斯定理(Menelaus theorem)：若在△ABC的三邊BC、CA、AB(或它們的延長線)上有三點X、Y、Z，則此三點共線的充分必要條件是

接下來證明Lemoine線(Lemoine line)：過三角形的項點作它的外接圓的切線與對邊相交，這樣的三個交點在同一直線上。

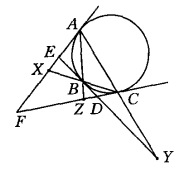
圖2

證明 如圖2，過A作△ABC的外接圓的切線AF交BC於點X，過B作外接圓的切線BY交AC於點Y，過C作外接圓的切線CF，交AB於點Z，我們要證明X，Y，Z三點在同一直線上，設BY交AF於E、交CF於D。

根據梅內勞斯定理，

∵直線XEF截△BCD，

∴

∵直線YDE截△ACF，

∴

∵直線ZDF截△ABE，

∴

⑴×⑵×⑶，得

又

由於X、Y、Z分別在△ABC的三邊之延長線上，故根據梅內勞斯定理知，X、Y、Z三點在同一直線上。