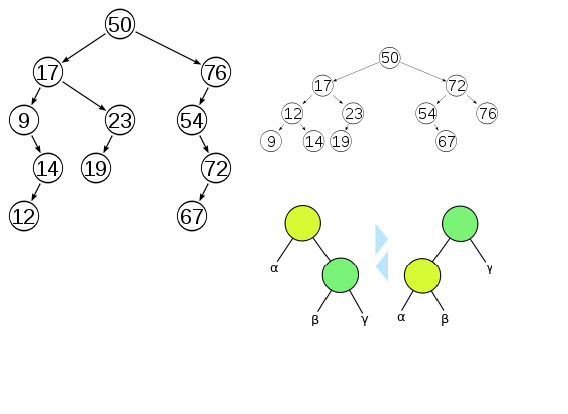
在計算機科學裡面,加權平衡樹(WBTs)是一種可以用來實現集合、字典(映射)和序列的平衡樹。這些樹結構在20世紀70年代被Nievergelt和Reingold作為有界限的自平衡樹。就像其他自平衡樹一樣,加權平衡樹儲存的賬簿信息可以在樹結構被插入和刪除操作打亂時,通過平衡結點和操作樹旋轉來使樹結構重新達到平衡。特別的地方是,加權平衡樹的每個結點儲存這個結點下子樹的大小,並且這個結點左右子樹的大小保持著某種內在聯繫。不同於AVL樹(儲存子樹的高度)和紅黑樹(儲存虛構的“顏色”位),加權平衡樹儲存記賬信息的方式是對套用真正有用的屬性:一棵樹下元素的數量等於它的根的大小,然而這個根的大小是一個用來實現順序統計樹操作的有用數據,也就是說,可以得到一個大小為n的集合下的最大元素或者決定一個順序結構下一個元素的索引。
基本介紹
- 中文名:加權平衡樹
- 外文名:Weighted balance tree
- 領域:計算機語言
- 定義:實現集合、字典和序列的平衡樹
- 有關術語:平衡樹
- 特點:平衡操作均攤開銷是恆定
簡介,平衡樹,函式式編程,
簡介
加權平衡樹是一種儲存子樹大小的二叉搜尋樹。那就是說,一個結點包含以下欄位:鍵(key),任何可排序的類型;值(value,可選,只作映射作用);左子樹(left),右子樹(right),結點的指針;大小(size),整數類型。從定義上來說,樹上葉子(沒有子結點的元素)的大小(典型地用一個空指針表示)是0。一個內部結點的大小是它的兩棵子樹的大小,再加一 (size[n] = size[n.left] + size[n.right] + 1)。一個結點的權重取決於它的大小或者等於它的大小,或weight[n] = size[n] + 1。
修改樹的操作必須使用與AVL樹中相同的操作來保證左子樹和右子樹的大小相互存在某種內在因子α,也就是旋轉和兩次選擇。形式上來說,結點平衡操作如下定義:如果一個結點滿足weight[n.left] ≥ α·weight[n]以及weight[n.right] ≥ α·weight[n],那么就說這個結點是α加權平衡的。
在這裡,α是一個在實現加權平衡樹是用來做決定的數值參數。α的值越小,意味著這棵樹“更加平衡”,但不是所有的α值都是合適的;Nievergelt和Reingold曾經證明過滿足

是一個平衡算法成功工作的重要狀態。他們往後的工作展示了α的一個下界是2⁄11,幾時它可以無限小如果使用一個自定義(更加複雜的)的再平衡算法。若平衡被正確實現,一棵含有n個元素的加權平衡樹的高度h滿足

加權平衡樹n次插入和刪除操作中,平衡的次數是線性的,為n。也就是說,加權平衡樹的平衡操作均攤開銷是恆定的。
平衡樹
平衡樹是二叉查找樹的一種,維持樹的平衡可以避免二叉查找樹的病態結構,減少查找路徑的平均長度,降低查找的時間平均複雜度。在1962年第一種平衡樹被發現,圍繞著更簡單的實現和更高的性能,提出了多種平衡樹,不同平衡樹的平衡調整策略往往不相同。最經典的平衡樹是AVL樹、加權平衡樹、替罪羊樹、伸展樹、隨機平衡樹、秩平衡樹等。AVL樹的性能是最優二叉查找樹與任意二叉樹的折衷,平衡程度嚴格,查找的時間複雜度低,適用於刪除插入操作較少的場合。平衡樹套用於表示有序的線性數據結構,如優先佇列、關聯數組、鍵-值的映射等。自平衡的二叉查找樹的實現與其競爭對手hash表的實現,各自具有優缺點。自平衡二叉查找樹在按序遍歷所有鍵值時是量級最優的,hash表不能。自平衡二叉查找樹在查找一個鍵值時,最壞情況下時間複雜度優於hash表, O(log n)對比O(n);但平均時間複雜度遜於hash表,O(log n)對比O(1)。
函式式編程
函式式編程(functional programming)或稱函式程式設計,又稱泛函編程,是一種編程典範,它將計算機運算視為數學上的函式計算,並且避免使用程式狀態以及易變對象。函式程式語言最重要的基礎是λ演算(lambda calculus)。而且λ演算的函式可以接受函式當作輸入(引數)和輸出(傳出值)。比起指令式編程,函式式編程更加強調程式執行的結果而非執行的過程,倡導利用若干簡單的執行單元讓計算結果不斷漸進,逐層推導複雜的運算,而不是設計一個複雜的執行過程。