剝皮法則是密度呈球對稱分布的法則。
基本介紹
- 中文名:剝皮法則
- 類別:法則
- 特點:密度呈球對稱分布
- 證明:球殼證明
球體,球殼,證明,
球體
球體(密度呈球對稱分布)內部空間的拓展——對球內任一距球心為r的一質點A的吸引力等效於質量與半徑為r的球的質量相等且位於球心的質點對質點A的吸引 。
球殼
球殼(密度呈球對稱分布)內部空間的拓展 ——對球殼內任一位置上任一質點A的吸引力都為零。
證明
球殼證明(球體可視為去掉球殼)
證明:設球殼內任一位置上任一質點A質量為m,對球內任一距球心為半徑的一質點的質量為M,取過A點的兩條弦(十分靠近)EC,BD.
令∠DAE=∠BAC=α→0,
則EA=DA,BA=CA
F(D對A)=(GMm)/AD ①
F(C對A)=(GMm)/AC ②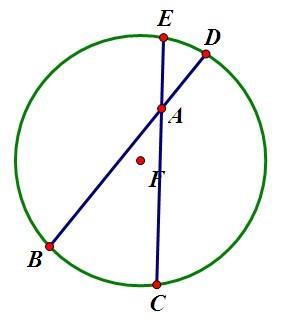

剝皮法則證明
由於上述夾角非常小,所以DE,BC之間的曲面可以視為一個圓(我只是淮南一中高一學生,不會求一部分球面對面積,所以只有近似,歡迎高手來修改為更好的解法)
S(DE之間)=π[1/2(ADα)] ③
S(BC之間)=π[1/2(ACα)] ④
F(ED之間的圓曲面對A)=①×③
F(BC之間的圓曲面對A)=②×④
上述兩式大小相等方向相反,合力為O
整個球殼以此類推
得,球殼對球殼內任一位置上任一質點A的吸引力都為零。
以上證明均為淮南一中2013屆學生證明,由於知識有限,如有不妥敬請見諒。
據說高等教育出版社出版的《力學》有相關嚴謹的證明,有需要有條件者可購買查閱
