剖分引理(splitting lemma)關於勢函式在退化定態點附近定性性質的重要命題.
基本介紹
- 中文名:剖分引理
- 外文名:splitting lemma
- 類型:數學術語
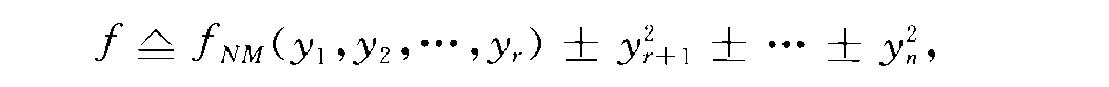
剖分引理(splitting lemma)關於勢函式在退化定態點附近定性性質的重要命題.
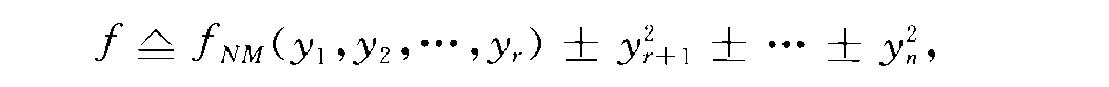
剖分引理(splitting lemma)關於勢函式在退化定態點附近定性性質的重要命題.在退化定態點上,勢函式的一階導數和黑塞矩陣的行列式同時為零,莫爾斯引理條件不成立,勢函式不能表為二次型.這時,若。點為光滑函式f:R...
它的二維情形是說:在單純剖分上的任何正常標號都有奇數個小顯三角形。這就是施佩納引理。它對於建立求一個連續映射的不動點的算法起了重要的作用。拓撲圖 拓撲圖是圖論的一個重要概念。能夠嵌入在某一拓撲空間T中的圖G稱為拓撲圖。即,圖G的頂點為拓撲空間T中的點,邊為連結其兩端點的簡單曲線,且任意兩邊...
突變芽是一種數學術語。突變芽(germ)突變理論術語.指勢函式分解之後決定突變特徵的部分.在突變理論中,按剖分引理可以把勢函式在退化臨界點處分解為莫爾斯(非退化)部分和一個最小的非莫爾斯部分,即V=M十 G(r).後者G(r)即為突變芽,其實質性變數個數為余維數:.法國數學家托姆(Thom,R. C.)的基本突變分類...
4.4 勢函式與剖分引理 4.4.1 Hessen矩陣與余秩數 4.4.2 剖分引理 4.4.3 萬能展開與余維數 4.5 基本突變類型 4.6 摺疊突變和尖點突變 4.6.1 摺疊突變 4.6.2 尖點突變 4.7 突變論的套用 4.7.1 在雷射中的套用 4.7.2 在彈性結構塌陷中的套用 4.7.3 在經濟系統中的套用 4.7.4 在...
引理1 同胚於圓盤與Mf;bius帶沿公共邊界的粘合。引理2Klein 瓶同胚於粘合了兩個 帶的球面。定理2(分類定理)任何光滑、緊緻、連通、閉、二維流形或同胚於有k 個柄的球面 ,或同胚於有s 個 膜的球面 。引理3任何二維、光滑、緊緻、連通、閉的M²允許有限的三角剖分。引理4詞W可以(藉助於M²的同胚)改造...
4.4 勢函式與剖分引理 4.5 基本突變類型 4.6 摺疊突變和尖點突變 4.7 突變論的套用 第5章 混沌學 5.1 混沌現象和混沌學 5.2 疊代與動力系統 5.3 非線性動力系統 5.4 邏輯斯蒂映射——混沌模型 5.5 從倍周期分岔到混沌 5.6 從區間映射到混沌的定義 5.7 混沌的結構特徵及規律性 5.8...
