切線模量

切線模量是指屈服極限和強度極限之間的斜率。在靜態應力-應變曲線上每點的斜率，稱為正切模量，一般來說某點的切線模量由該點附近應力變化量與應變變化量之比進行計算。塑性材料不同於金屬材性，它具有黏彈性，應力-應變曲線是非線性的，因而每點的切線模量也就不同。

基本介紹

• 中文名：切線模量
• 外文名：Tangent modulus
• 描述：屈服極限和強度極限之間的斜率
• 套用：考察材料力學性能
• 學科：物理

概念

切線模量就是屈服極限和強度極限之間的斜率，用於雙線性彈塑性模型來考慮材料的性能。工程上希望知道其相關模量，從而提出切線模量，是材料非彈性極限範圍內的巨觀的模量的一種表述。根據定義可知，該模量為材料發生屈服以後的硬化模量，可以通過拉伸實驗來確定的。它與彈性模量的比值稱為塑形係數，在各種結構計算比如局部穩定計算中會用到。

例如Q235鋼材，彈性模量為2.03×E⁰⁵MPa，泊松比為0.3，鋼材密度是7850kg/m³，切線模量為6100MPa，阻尼比取0.02。

黏土非線性模型的改進切線模量

岩土工程數值計算結果是否可靠和符合實際，與計算所選用的土體本構模型密切相關，而土體應力應變行為的描述及切線模量的表征又是土體本構模型的核心問題。基於雙曲線應力應變曲線描述的鄧肯非線性土體模型由於簡潔直觀，並能較好的反映土體的非線性特性，且參數易於通過試驗直接獲得，因而最為常用。但該模型採用簡單雙曲線描述應力應變曲線有時存在很大誤差，導致切線模量的模擬結果與實際情況存在較大的差異。研究基於微分方程建立了土體參數應力應變新模型，改進了非線性切線模量的表達，為進一步研究土體本構模型奠定了基礎。

雙曲線應力應變模型分析

大量試驗數據表明雙曲線並不能很好的模擬三軸試驗的應力應變關係，有時存在很大誤差。這種誤差的根本原因在於雙曲線的局限性，下面引入應力應變曲線的另一個特徵量“半值強度指數”分析此問題。定義三軸試驗應力應變曲線的“半值強度指數”為：“當土體偏應力達到對應極限偏應力的1/2時，對應的應變數值。由此定義可知，它是以應變的形式描述土體應力發展速度的又一特徵量，對按變形設計的現代岩土工程課題非常重要。半值強度指數越小，土體應力相對發展速度越快，參見圖1。

圖 1 土的應力應變關係曲線

在雙曲線模型中隱含了“半值強度指數在數值上等於極限偏應力與初始切線模量之比”這一冗餘條件，這是產生較大擬合誤差的根本原因。實際上即使在極限強度與初始切線模量確定的情況下，半值強度指數還可能與土體自身性質、外界條件等因素有關。較為理想的應力應變模型應能保證3個特徵方程獨立，在極限強度與初始切線模量確定的情況下仍能夠強度的發展速度。

非線性切線模量改進

切線模量建立的主要工作就是確定參數應力應變模型中待定參數與土體基本參數的關係。以下採用3參數新應力應變模型對土體切線模量進行改進。

（1）模型參數的確定

由以上分析可知，a 即為土體的極限偏應力。實際上ε不可能無窮大，在達到一定值后土體就破壞了，這時的偏應力為 (σ₁ - σ₃)f ，它總是小於極限偏應力。試驗數據的擬合表明，對於初始狀態相同的土體，不同圍壓下參數 b 與 a 的比值基本不變，即ba = λ ，其中λ 為不小於 1 的實數。

表 1 土體改進切線模量參數

（2）試驗數據模擬

聯立模型參數可以得到改進剪下模量對應的不同圍壓下的土體應力應變曲線。對文獻中的一組三軸試驗數據進行模擬，結果見圖2，模型參數取值見表1。由圖2可見，本文提出的改進模型能夠很好的模擬土體應力應變曲線，需要說明的是，傳統雙曲線模型由於自身的局限性無法得到圖2中理想的模擬結果。

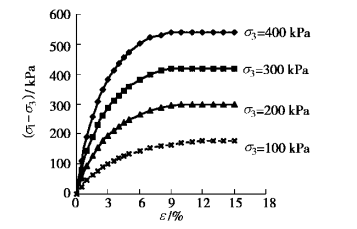圖2 土體應力應變曲線模擬

研究結論

土體應力應變模型和切線模量的模擬是土體非線性模型的基本問題，是岩土工程數值分析的前提條件，研究對此作了較為詳細的研究。

（1）在傳統初始切線模量、極限偏應力的基礎上，引入“半值強度指數”的概念，建立了應力應變模型的數學特徵方程，分析了雙曲線應力應變模型數學特徵方程不獨立的缺陷。

（2）在試驗數據分析的基礎上，提出了土體應力應變曲線的控制微分方程，進一步建立了3參數新應力應變模型，該模型數學性質與理想應力應變曲線吻合。

（3）從數學上嚴格證明了雙曲線模型是3參數新應力應變模型的特例。

（4）在 3 參數新應力應變模型的基礎上，改進了非線性模型中土體切線模量的表達，給出了確定參數的方法，並採用改進的切線模量對 3 軸試驗數據進行了模擬。

用雙曲線切線模量方程計算地基非線性沉降

現有的地基沉降計算方法包括弦線模量法，在確定地基的應力分布時，均是按彈性介質考慮，而地基是非彈性介質，因此，理論附加應力與實際應力有偏差。一般認為，根據 Boussinesq 彈性應力解計算得到的應力分布是偏大的，因此，採用彈性應力解計算得到的沉降將會偏大，弦線模量法為了得到比較準確的沉降結果，在計算地基沉降時，採用的是前一級荷載稍稍偏大的模量值。

研究依據載荷試驗曲線對附加應力進行修正，確定出新的變形參數——雙曲線切線模量（又稱修正切線模量）來計算地基的沉降，能夠得到與試驗值完全吻合的結果，該方法計算原理簡單，適用於各類地基土，將為地基沉降預測開闢出一條新途徑。

切線模量方程及沉降計算公式

假定地基為非均質非線性的彈性體，而各分層土則看作是各向同性彈性體，分段載入過程中每段載入均可視為線性彈性體。原位土體的變形模量E₀可根據載荷試驗試驗曲線起始直線段某壓力點p₁對應的沉降量 s₁ 利用下列公式計算得到：

式中：I₀ = ωd，ω 為剛性承壓板的形狀係數，圓形承壓板取0.79;方形承壓板取0.88；d 為承壓板的直徑或邊長；µ為土的泊松比。

理論研究表明，基礎埋深對附加應力分布有影響。由於基礎底面平面上存在剪下摩擦力，導致地基內荷載作用中心下地基內的豎向附加應力p_z減少10%左右，按照彈性理論計算得到的附加應力是偏大的；而土體的非線性非均質特徵也會對附加應力分布產生一定影響。

對於大型筏板基礎或大面積堆載情況，由於附加應力分布範圍深厚，對不同的土層（或厚度較大的同一土層的分段土層）需做深層的螺旋板載荷試驗或旁壓試驗以確定各層土的切線模量方程。旁壓試驗實際上是一種側向載荷試驗，分預鑽式和自鑽式2種。自鑽式旁壓試驗雖然成果更加可靠，但儀器操作複雜、價格高，故預鑽式旁壓試驗套用較多。

研究結論

（1）對於幾個不同地點、不同土類型、不同壓板形狀尺寸的載荷試驗，採用雙曲線切線模量計算得到的地基沉降，與實測曲線吻合得很好，說明雙曲線切線模量是能夠準確計算地基沉降的理想參數；

（2）切線模量方程包含了載荷試驗及沉降計算參數的全部信息，且形式簡單，物理意義明確，能夠反映地基的非線性變形特徵，可用於載荷試驗成果的整理、分析，並為地基非線性沉降計算提供附加應力之外的充分必要之依據；

（3）切線模量的大小與附加應力水平有關，附加應力修正係數β值一般在 0.85～1.0之間，說明附加應力分布採用彈性理論公式進行計算其誤差一般在15%以內；β值用載荷試驗數據進行雙曲線擬合後自動求解，計算過程不受人工因素干預影響；壓縮層計算深度與分層厚度可以不受限制；

（4）與其他計算方法相比，本方法計算原理簡單，計算結果準確，計算參數全部來自原狀土測試資料，較為可靠。分段雙曲線擬合法能夠求解載荷試驗曲線與雙曲線相關性不高的情況；

（5）規範法中的沉降計算經驗係數ψ 未充分考慮附加應力水平的影響，是造成計算結果誤差偏大的主要原因。

鑒於承載機制的相似性，本方法對於小面積基礎（如獨立基礎、條形基礎）的沉降計算無疑是適用的。對於套用雙曲線切線模量求解大尺寸基礎 （如筏板基礎）或大面積堆載以及複合地基情況下地基沉降問題的準確性還有待進一步的驗證，此外，推導出能夠考慮時間因素的雙曲線切線模量方程也是值得進一步研究的課題。