分離係數法

多項式的分離係數法(method of detached coefficients of polynomials)是多項式四則運算的一種演算形式。對一元多項式進行加、減、乘、除運算時，首先將多項式寫成標準形式並按變元降冪或升冪排列，缺項補零占位，然後略去各項的變數字母，分離出各項的係數，僅用係數組成的數列按原運算的意義進行運算，最後將運算所得數列中各數分別配上與之相應項的變數字母的冪作為運算的最後結果，稱為多項式的分離係數法。

基本介紹

• 中文名：分離係數法
• 外文名：The separation coefficient method
• 所屬學科：數學（代數學）
• 所屬問題：初等代數(代數式)
• 套用：代數式的運算

基本介紹

當按豎式計算兩個多項式，兩個多項式進行加減法運算時，只須對同類項的係數之間進行加減法運算，與變數無關，因此可以把多項式只寫出它們的係數進行加減法運算，更為簡便，這種方法叫做分離係數法。

舉例分析

例1計算 ，可以如下進行：

結果是 。

對於乘法或除法也可用分離係數法進行。例如，計算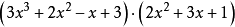

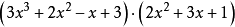
解：

結果是 。

在套用分離係數法進行運算時，注意運算結果的次數，遇有缺項時要空位或補上0，而且兩個多項式都要按降冪順序排列，否則容易出錯。

例2 求 和 的乘積。

解：先按 降冪排列，只寫出係數，缺項處補充以0，在最後的結果中填入 的適當方冪(從 開始，因為積的最高次項的次數是6)。

所以解得 。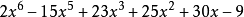

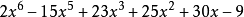
例3 證明恆等式：

解：先按a的降冪、b的升冪排列。用分離係數法，最後結果中乘積的最高次項的次數是5。

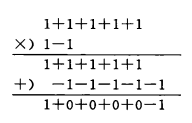
所以