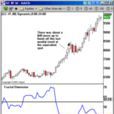
分維指標是分數維數(Fractal Dimension)基礎上算出的指標,套用於分析。
基本介紹
- 中文名:分維指標
- 相關:參考連線和內容
- 類型:數學
- 基礎:分數維數
- 套用:分析
指標直接相關參考連線和內容,參考文獻,
指標直接相關參考連線和內容
“從 1.1到1.9分維越來越大,如果盤整明顯則分維指標值高,然後變盤後的趨勢越明顯,所以能構成市場延伸的測度.又因為分維指標計算和均線有共同短處,所以分維指標來不及稀釋,強趨勢時,往往要一跌再跌才達到0.35以下,趨勢終止也要慢慢等盤整度量比例加大才重回0.5一線。”
附:分維的解釋
1.分形(Fractal)是指具有自相似特性的現象、圖像或者物理過
程等。分形學誕生於 1970年代中期,屬於現代數學中的一個分
支。分形學的創始人是具有法國和美國雙重國籍的曼德勃羅(就是波努瓦·芒德勃羅) ,
他在1982年出版的<大自然的分形幾何學> (The Fractal
Geometry of Nature)是分形學的經典著作。 分形一般有以下
特質:
分形有無限精細的結構,即有任意小比例的細節
分形從傳統的幾何觀點看如此不規則,以至於難以用傳統的幾
何語言來描述
分形有統計的或近似的自相似的形式
分形可以由簡單的方法定義,例如疊代
分形的維數(可以有多種定義)大於其拓撲維數
2.分維反映分形的複雜性特點,通過計算可得分形的維數(分
維)值。
參考文獻
[1] Mandelbrot,B.B.,1967,How long is the coast of
Britain? Statistical selfsimilarity and fractional
dimension,Science,155,636~638
[2] Mandelbrot,B.B.,1977,Fractals,Form,Chance and
Dimension,San Francisco,W.H.Freeman&Co.
[3] Mandelbrot,B.B.,1982,The Fractal Geometry of
Nature,San Francisco,Freeman.
[4] 李水根,2004,分形,北京:高等教育出版社