分式模(fractional module)模論的重要概念之一它是由模所產生的新模,是分式環概念的推廣.若A是交換環。
介紹
分式模(fractional module)模論的重要概念之一它是由模所產生的新模,是分式環概念的推廣.若A是交換環,s是A的乘法封閉子集,並且iEs,o百s,則可以得到A關於s的分式環s-lA.設M是左A模,積MXS={(二,、)l二〔M,sES},若存在、ES,使得、(sex,一、,x})=0,則定義(二:,s,)^-(二:,sZ).這是一個等價關係,由此產生的商集記為S-'M,它的元素記為x/s,xEM,sES.再定義: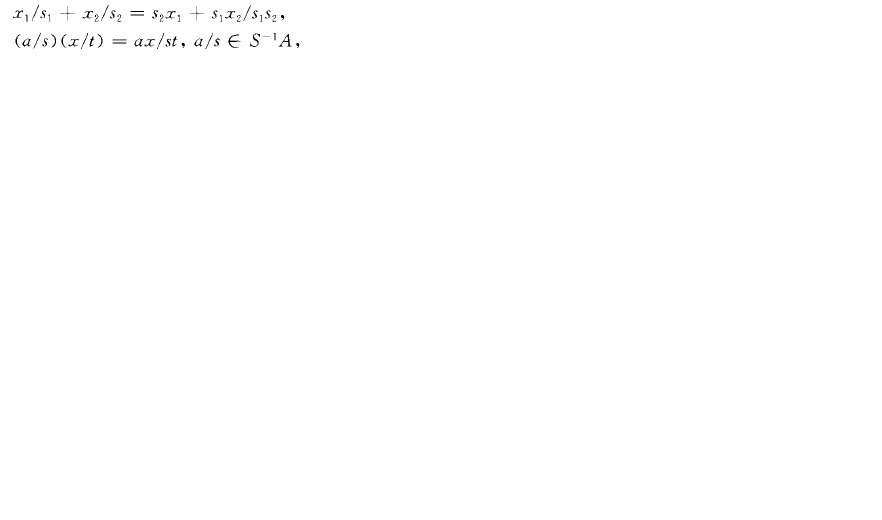
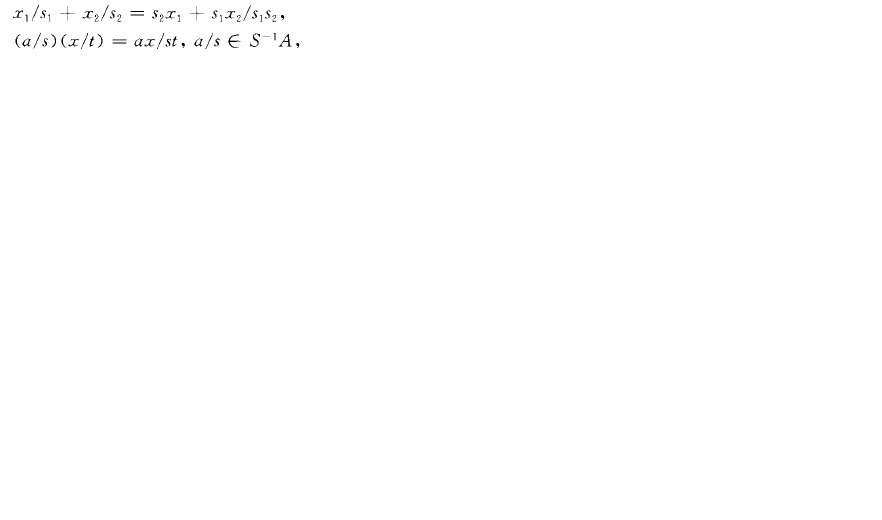
從而可得到s-'A模S -' M,稱為M關於S的分式模,也稱為M關於S的局部化.M與S-' M有著密切的聯繫,例如:對環A的任何極大理想m,記S=A\m , S-' M= Mm,若對一切極大理想m皆有M}, _0,則M= 0.分式環和分式模的概念都可推廣到非交換環的情況,它們分別稱為商環和商模,它們與撓理論有密切聯繫.
