分區平差(block adjustment)平差計算中的方法之一它是利用法方程係數陣的稀疏性結構而形成的一種分組平差方法.所謂分區是指將一個大型測量網劃分成若干個獨立的部分,每個部分即稱為一個區一般而言,如果整體平差時的法方程具有如下矩陣結構形式: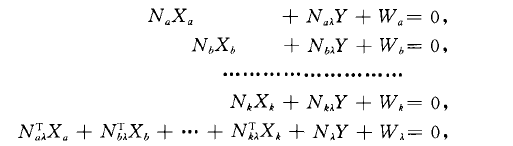
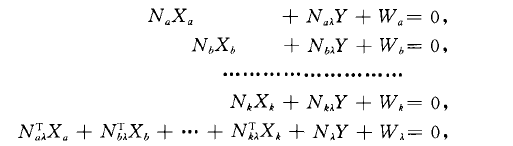
即可採用分區平差的方法進行計算.上式中前k個矩陣方程分別與各個分區相對應,最後一個方程稱為聯繫方程.XafXbf...}Xk稱為內部(或區域性)未知數,Y稱為公共未知數.
分區平差的實際計算步驟是:
1.分區後分別列出其方程式並組成法方程,消去內部未知數,得到各分區的約化法方程.
2.將各區的約化方程的係數和常數項對應相加,得到只包含公共未知數Y的聯繫約化方程,並由它解出Y.
3.將得出的Y值分別回代到各分區的約化方程,求出其內部未知數Xa,Xb,'. .
從理論上可以證明,這樣計算的結果將與整體平差的結果完全相等.
分區平差的實際計算步驟是:
1.分區後分別列出其方程式並組成法方程,消去內部未知數,得到各分區的約化法方程.
2.將各區的約化方程的係數和常數項對應相加,得到只包含公共未知數Y的聯繫約化方程,並由它解出Y.
3.將得出的Y值分別回代到各分區的約化方程,求出其內部未知數Xa,Xb,'. .
從理論上可以證明,這樣計算的結果將與整體平差的結果完全相等.
