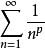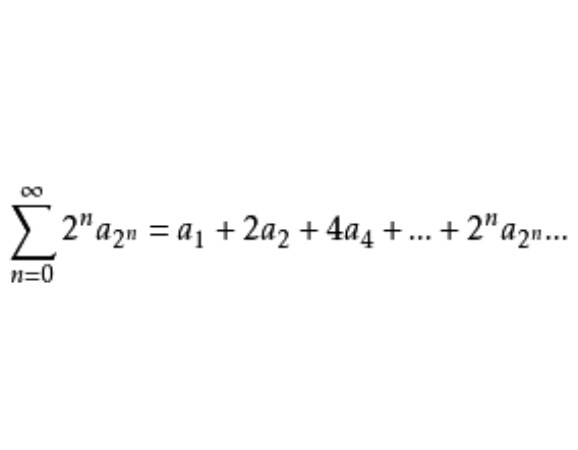基本介紹
基本介紹,凝聚判別法的證明,例題解析,
基本介紹
Cauchy凝聚判別法 級數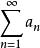 收斂的充分必要條件是:凝聚項級數
收斂的充分必要條件是:凝聚項級數
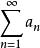
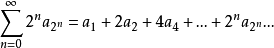
凝聚判別法的證明
證明 記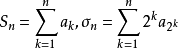 ,則
,則
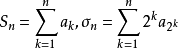
(1)當 時,我們有
時,我們有

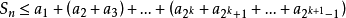

(2)當n>2k時,我們有
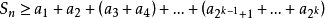
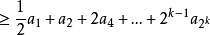
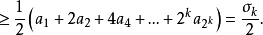
若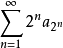 收斂於
收斂於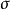 ,則由(1)知
,則由(1)知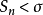 ,這說明Sn有界,即
,這說明Sn有界,即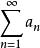 收斂。
收斂。
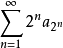
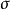
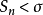
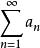
若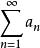 收斂於S,則由(2)知
收斂於S,則由(2)知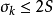 ,這說明
,這說明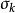 有界,即
有界,即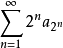 收斂。
收斂。
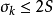
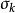
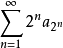
例題解析
【例1】級數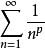 在p≤1時發散,p>1時收斂。
在p≤1時發散,p>1時收斂。
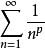
證明 (1)當p≤0時, ≥1,該級數顯然發散。
≥1,該級數顯然發散。

(2)當p>0時,{ }是遞減正數列,從而考察級數
}是遞減正數列,從而考察級數


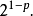
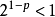
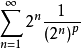
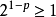
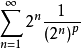
根據Cauchy凝聚判別法,即得所證。
注 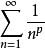 俗稱p-級數,是級數論中最重要的範例之一,許多級數斂散性的判定常以它作為比較的標準。
俗稱p-級數,是級數論中最重要的範例之一,許多級數斂散性的判定常以它作為比較的標準。