再生核又稱為重建核,它定量地給出了小波基的相關性和冗餘性。如果變換係數之間有一定的相關性(不正交),就可能從其中一個變換係數恢復(或再生)出另外一個變換係數,因此,再生核的稱謂由此得來。
基本介紹
- 中文名:再生核
- 適用範圍:數理科學
簡介,推論,再生核方程,
簡介
再生核又稱為重建核,它定量地給出了小波基的相關性和冗餘性。
從小波基函式的定義可以猜想,如果a,τ參數連續變化,得到的小波基將是冗餘的。或者這樣理解:如果在尺度-位移平面上的兩個點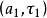 和
和 很靠近,那么得到的小波基函式
很靠近,那么得到的小波基函式 和
和 形狀和大小很接近,位置也很靠近,它們具有很強的相關性,而且隨著兩個點的更加靠近,相關性增強,反之則相關性減弱。存在相關性就意味著不正交(因為根據機率論的知識,正交必定不相關),因此就存在著冗餘。
形狀和大小很接近,位置也很靠近,它們具有很強的相關性,而且隨著兩個點的更加靠近,相關性增強,反之則相關性減弱。存在相關性就意味著不正交(因為根據機率論的知識,正交必定不相關),因此就存在著冗餘。
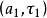



推論
尺度-位移連續變化的小波基函式 形成了一組非正交的過度完全基。其中的“過度”表示這一組基含有冗餘性,“完全”表示這一組基可以完全覆蓋整個尺度一位移平面,這樣,任意一個信號都可以用這些基來分解表示。在 a-τ平面上任意兩點
形成了一組非正交的過度完全基。其中的“過度”表示這一組基含有冗餘性,“完全”表示這一組基可以完全覆蓋整個尺度一位移平面,這樣,任意一個信號都可以用這些基來分解表示。在 a-τ平面上任意兩點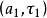 和
和 ,其對應的小波基函式之間究竟有多大的相關性,這就需要用再生核來描述和刻畫。從再生核的定義式,即
,其對應的小波基函式之間究竟有多大的相關性,這就需要用再生核來描述和刻畫。從再生核的定義式,即

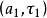


可以看出,式(1)實質上是計算函式內積 ,只是比例係數稍有不同。在數學上,內積實質上表示了兩個函式的“相似”程度。如果兩個信號矢量
,只是比例係數稍有不同。在數學上,內積實質上表示了兩個函式的“相似”程度。如果兩個信號矢量 與
與 完全垂直,那么內積
完全垂直,那么內積 再生核
再生核 表示兩個信號矢量完全不相關。如果矢量
表示兩個信號矢量完全不相關。如果矢量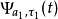 與
與 完全平行,那么內積
完全平行,那么內積 和再生核
和再生核 都分別取得最大值,表示兩個信號矢量完全相關。式(1)中的係數為
都分別取得最大值,表示兩個信號矢量完全相關。式(1)中的係數為





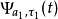













再生核方程




式(4)稱為重建核方程(或再生核方程)。
