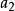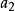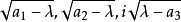基本介紹
- 中文名:共焦二次曲面族
- 外文名:family of confocal quadric surface
- 屬性:有重要意義的二次曲面族
- 分類:橢球面、單葉雙曲面等
- 別稱:共焦族
基礎知識,橢球,單葉雙曲面族,雙葉雙曲面族,
基礎知識
設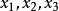 是空間
是空間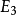 的點的直角坐標,由方程
的點的直角坐標,由方程
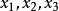
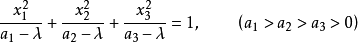




4.當 介於
介於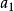 與
與 之間時,上列方程表示虛曲面。
之間時,上列方程表示虛曲面。

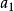

橢球
現在我們將闡明共焦曲面族的一個明晰的表示,而且首先從橢球著手,它的三個半軸之長顯然是
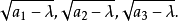
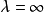
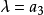
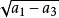
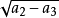

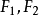
 圖1
圖1單葉雙曲面族
 圖2
圖2這個雙曲面族一方是由一個作為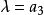 時的極限的雙曲面塊所圍成,後者並充滿著焦橢圓的外部;另一方是由一條作為
時的極限的雙曲面塊所圍成,後者並充滿著焦橢圓的外部;另一方是由一條作為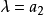 時的極限的焦雙曲線外部所構成,就是圖2中附上陰影線部分,這條雙曲線落在
時的極限的焦雙曲線外部所構成,就是圖2中附上陰影線部分,這條雙曲線落在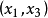 平面上而且具有下列方程:
平面上而且具有下列方程:
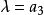
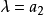
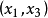

在上列兩極限位置之間充滿著其餘的單葉雙曲面,使其全體圍繞著焦雙曲線而被焦橢圓所局限著。
雙葉雙曲面族
最後,我們還要觀察雙葉雙曲面族,各曲面的實軸重合於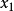 軸,這族圍成
軸,這族圍成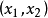 平面中,如圖3所示的焦雙曲線內部的陰影部分,作為在
平面中,如圖3所示的焦雙曲線內部的陰影部分,作為在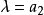 時的極限情況,但是當
時的極限情況,但是當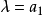 時的第二極限情況是作為雙重計算的
時的第二極限情況是作為雙重計算的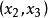 平面,在其上已不存在焦曲線,因為方程
平面,在其上已不存在焦曲線,因為方程
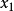
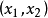
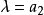
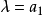
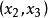
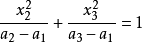
此外,雙葉雙曲面族也是恰恰一度地充滿著整個空間,而實際上是這樣:一個外殼總是圍繞著焦雙曲線的右支,而且另一個外殼則圍繞著左支。