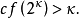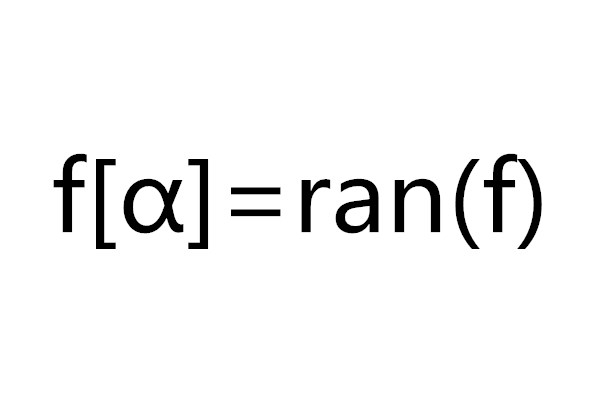共尾函式

共尾函式(cofinal function)是一類特殊的序數的函式，設f是序數β到α的函式，若f的值域在α內無界，即∪ran(f)=α，則稱f在α內共尾。若對在α內共尾的遞增序數序列{α_λ}_λ<β，令f(λ)=α_λ，則f是α內的共尾函式。

基本介紹

• 中文名：共尾函式
• 外文名：cofinal function
• 所屬學科：數學
• 所屬問題：樸素集合論（序數）
• 簡介：一類特殊的序數的函式

基本介紹

定義 設β是極限序數：

(1)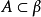在β內是無界的，如果∪A=β;

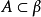
(2)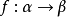是一個共尾函式，如果f[α]=ran(f)在β內是無界的。

相關概念及定理

定義1 共尾子集是序數的一種重要子集，若A是序數α的子集，且sup A=α，則A稱為在α中共尾的子集，若函式f：β→α在α中共尾，則值域ran(f)是在α中共尾的子集。若α的任何共尾子集A的標號集為β，且A={α_λ}|_λ≤β，則由f(λ)=α_λ定義的函式f：β→α是在α中共尾的函式。

定義2 極限序數β的共尾度cf(β)定義如下：

cf(β)=min{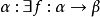是共尾函式}。

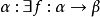
顯然cf(β)≤β。

引理3 設β是極限序數，則存在嚴格增的共尾函式：

f：cf(β)→β。

證明: 設g：cf(β)→β是任意的共尾函式。定義：

f(η)=max{g(η)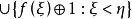，}，η∈cf(β)．

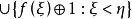
易知f：cf(β)→β是嚴格增的共尾函式。

證畢。

引理4 設α，β是極限序數。

(1) 若存在嚴格增的共尾函式g:α→β，則cf(α)=cf(β).

(2) cf(α)是極限序數且cf(cf(α))= cf(α).

(3) cf(α)=cf(ω_α)。

證明： (1)設h: cf(α)→α是共尾函式，則

是共尾的,從而cf(β)≤cf(α).

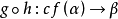
另一方面,設f:cf(β)→β是共尾函式,定義:

易知k:cf(β)→α是共尾函式,從而cf(α)≤cf(β)。

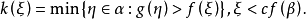
故cf(α)=cf(β)。

(1)與(2)由(3)知。

證畢。

定義 一個極限序數β是正則的，如果cf(β)=β。

易知cf(β)是正則的。

引理 (1) ω是正則的。

(2) 若極限序數β是正則的，則β是基數。

(3) 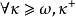是正則的。

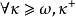
引理 ( I ) (König)若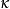是無限基數且cf(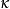)<λ,則.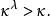

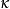
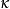
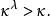
(2) 若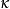是無限基數,則