八進制數，就是用八進制記下的數稱為八進數或八進位數。八進數可用符號 ( )8 來表示。
符號8和9不用在八進制系統中。在oct 7後跳到oct 10。似乎有些混亂，但oct 10實際與dec 8相等，oct 11表示的是dec 9。
數oct 31能轉換為bin 011001，然後轉換為十進制。
基本介紹
- 中文名：八進數
- 外文名：octal number
- 適用範圍：數理科學
- 作用：邏輯運算
簡介,引入,定義,八進數的轉換,用法,
簡介
引入
八進制是特殊的記數進位制之一。在位值制記數法中，依據逢八進一點法則，使用 0，1，2，3，4，5，6，7八個數字計數，這種記數法稱為八進制記數法或八進位記數法，簡稱八進制或八進位制。
定義
用八進制記下的數稱為八進數或八進位數。八進數可用符號 ( )8 來表示。
八進數的轉換
將一個十進數化為八進數，可用基數 8 連續去除十進數，反序取餘數就是要求的八進數。
例如，把 (321)10 化為八進數：
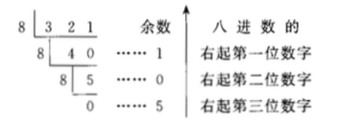圖1.所以把 (321)10=(501)8。
反之，任何一個八進數，都可以寫作基數為 8 的冪的和的形式，再按十進數的計算法則算出結果，就得到對於的十進數。例如，把(501)8化為十進數：
| 八進數 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 二進數 | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
利用上表不難完成二進數與八進數之間的換算。例如 (1010001110)2=(1216)8。
用法
符號8和9不用在八進制系統中。在oct 7後跳到oct 10。似乎有些混亂，但oct 10實際與dec 8相等，oct 11表示的是dec 9。
見上表，數oct 31能轉換為bin 011001，然後轉換為十進制。
bin 011001=(0×25)+(1×24)+(1×23)+(0×22)+(0×21)+(1×20)=dec 25
按八進制記數的數。
在八進制數中，每一位用0-7八個數碼錶示，所以它的計數基數為8。
低位數和高一位數之間的關係是逢八進一。
十進制、二進制、八進制之間存在一定的對應關係。
同樣一個數用八進制寫出的結果要比用二進制寫出的結果簡單得多。
十進制數與八進制數的轉換
(96)10=(140)8
(85)10=(125)8
算法:除八取余
96 0
12 4
1
倒序排列140
85 5
10 2
1
倒序排列125
八進制數與二進制數的轉換
(76)8=(111110)2
一位換三位
(7)8=(111)2
(6)8=(110)2
(5)8=(101)2
(4)8=(100)2
(3)8=(011)2
(2)8=(010)2
(1)8=(001)2
