克立金法,又稱克立金法變差函式,適用於地質變數研究。用變差曲線表示、
基本介紹
- 中文名:克立金法
- 別稱:克立金法變差函式
- 表達式:使估計誤差為最小。
- 提出者:克立格
- 套用學科:地質
- 適用領域範圍:地質變數
- 原理:克立金法基本原理
- 套用:變差曲線表示
基本原理,變差函式,
基本原理
克立金法最初是由南非金礦地質學家克立格(D.G.Krige)根據南非金礦的具體情況提出的計算礦產儲量的方法;按照樣品與待估塊段的相對空間位置和相關程度來計算塊段品位及儲量,並使估計誤差為最小。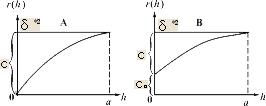

克立金法基本原理是根據相鄰變數的值(如若干樣品元素含量值),利用變差函式所揭示的區域化變數的內在聯繫來估計空間變數數值的方法。
地質變數是區域化變數,具有空間結構性,即在空間點x和x+h 處的變數值 Z(x)和Z(x+h) 具有自相關性。這種相關依賴於兩點間的向量h和礦化特徵。區域化變數的空間特徵由變差函式來描述。
變差函式
變差函式為區域變數 Z(x)的增量平方的數學期望,即區域化變數增量的方差。變差函式即是距離 h的函式,又是方向a的函式,通式可寫成:
2r(h,a)=2r(h)=E{{z(x)-z(x+h)}2}
變差函式一般以變差曲線表示。由圖可見,隨著 h的增大,r(h)趨於穩定值,這時的h稱為變程,記為a,它表示了變數從空間相關狀態到不相關狀態的轉折點,而r (a)稱為基台值(c+c0)。變程揭示了變數空間自相關性的影響範圍,基台值反映了變數變異的強弱。當h趨於零時,r(h)的極限值即曲線在縱坐標的截距為塊金常數(c0),它反映了變數隨機性的大小。
