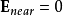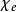克勞修斯-莫索提方程是關於解釋分子α的極化性與介電常數ε（在這種極化性中由分子組成的電介質物質）的關係。
基本介紹
- 中文名：克勞修斯-莫索提方程
- 外文名：Clausius-Mossotti equation
- 套用學科：物理
- 定義：極化性和相對電容率間的關係
簡介,導引,參閱,
簡介
克勞修斯-莫索提方程（Clausius-Mossotti equation）表達了線性介電質的極化性和相對電容率之間的關係，是因義大利物理學者莫索提（Ottaviano-Fabrizio Mossotti）和德國物理學者魯道夫·克勞修斯而命名。這方程式也可以更改為表達極化性和折射率之間的關係，此時稱為洛倫茲-洛倫茨方程式（Lorentz-Lorenz equation）。
導引
一個分子的極化性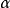
定義為
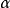
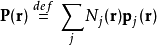
其中，P是電極化強度，r是檢驗位置，
分別是分子j的數量每單位面積與電偶極矩。
總合介電質內每一種分子的貢獻，就可以計算出介電質的電極化強度。將極化性的定義式代入，可以得到
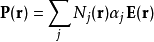
當計算這方程式時，必需先知道在分子位置的電場，稱為“局域電場”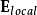
。介電質內部的微觀電場，從一個位置到另外位置，其變化可能會相當劇烈，在電子或質子附近，電場很大，距離稍微遠一點，電場呈平方反比減弱。所以，很難計算這么複雜的電場的物理行為。幸運地是，對於大多數計算，並不需要這么詳細的描述。所以，只要選擇一個足夠大的區域（例如，體積為V'、內中含有上千個分子的圓球體V '）來計算微觀電場
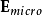的平均值，稱為“巨觀電場”
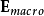，就可以足夠準確地計算出巨觀物理行為：
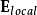
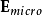
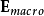
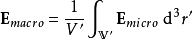
對於稀薄介電質，分子與分子之間的距離相隔很遠，鄰近分子的貢獻很小，局域電場可以近似為巨觀電場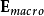 
：
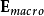
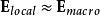
但對於緻密介電質，分子與分子之間的距離相隔很近，鄰近分子的貢獻很大，必需將鄰近分子的貢獻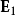
納入考量：
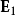
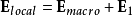
因為巨觀電場已經包括了電極化所產生的電場（稱為“去極化場”）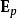
，為了不重複計算，在計算
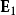時，必需將鄰近分子的真實貢獻
減掉去極化場：
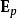
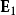
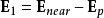
現在思考以分子位置r為圓心、體積為V'的圓球體V'，感受到外電場的作用，V'內部的束縛電荷會被電極化，從而產生電極化強度P。假設在V '內部的電極化強度P相當均勻，則電極化強度P與V'的電偶極矩之間的關係為
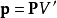
這線性均勻介電質圓球體內部的電場為
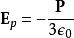
綜合前面得到的結果：
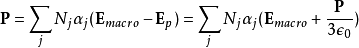
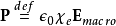
電極化率與極化性的關係為
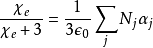
由於相對電容率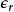
與電極化率的關係為
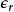
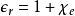
所以，電容率與極化性的關係為
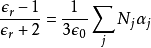
這方程式就是克勞修斯-莫索提方程式。
電介質的折射率n為
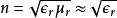
其中，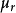
是相對磁導率。
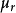
對於大多數介電質，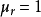
，所以，折射率近似為
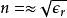。將折射率帶入克勞修斯-莫索提方程式，就可以給出洛倫茲-洛倫茨方程式：
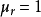
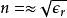
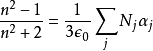
參閱
- 高介電常數材料(High-k)
