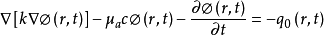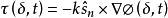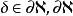光擴散方程

擴散(漫射)方程(diffusion equation ,DE)模型是對輻射傳輸方程的一階球諧展開近似，由於它最終表示為相對簡單的橢圓形偏微分方程形式，特別適用於諸如有限差分或有限元等數值方法有效求解。因而該模型可模擬任意幾何形狀和光學參數分步下的組織體內的傳播行為。

擴散模型的推導已廣見於許多文獻與教材中，其中共同步驟是將輻射率φ(r, ŝ，t)、散射相位函式р（ŝ，ŝ’）和光源項Q（r，ŝ，t）用球諧函式展開。

上述三式記為⑴，式中 （ŝ）為球諧函式； 為展開係數。對⑴式展開並取n=1，即對n>1，，.上述步驟即時取一階近似，擴散方程也因此稱為近似。

記為⑵式，將ŝ用球諧函式展開，⑵式進一步變為：

記為⑶式，式中J(r,t)為通量密度矢量或光子流。同理，對輻射傳輸方程的原項q(r, ŝ，t)作近似，有

記為⑷式，式中

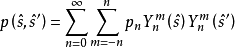
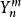
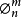
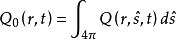
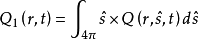
上述兩式記為⑸。

在下面的推導中，為了簡單起見，光子能量密度，用光子密度直接表示；相應地，光源項以光子密度源的形式表示，即q（r,t）=(r,t)。將式⑶和⑷代入⑸可得：

記上式為⑹，並對其進行全立體角積分可得：

記上式為⑺，並且⑺式常稱為連續方程。將⑺式等號兩邊同時點乘ŝ，對全立體角積分可得：

記上式為⑻，式中稱為約化散射係數，且有：

記上式為⑼，式中g為前面所定義的平均散射餘弦。為最終獲得擴散方程的表示式，我們作以下兩點假設：

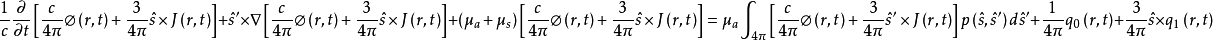
①：假設源為迷向的，即：

②：假設光流J的相對時間變化率遠小於擴散損失：

上述兩式分別記為⑽⑾，並將該假設導致式⑻退化為Fick定律：

記為式⑿，該式中k定義為：

記為式⒀。將式⑿代入式⑺即可得到時變擴散方程：

記為式⒁。根據式⑿，組織體表面檢測到的輸出光流量（通量密度）為：

記為式⒂，其中，為表面測量點位置，即代表組織體表面；為表面外法相單位矢量。