傑克森定理

傑克森定理是用函式的構造性刻畫其最佳逼近值的階的定理，是傑克森(Jackson,D.)在1912年建立的。

基本介紹

• 中文名：傑克森定理
• 外文名：Jackson theorem
• 適用範圍：數理科學

簡介

傑克森定理是用函式的構造性刻畫其最佳逼近值的階的定理。

這是傑克森(Jackson,D.)在1912年建立的，人們稱之為傑克森定理。

具體內容

設f∈C[a,b]，ω(f,δ)是f的連續性模，E_n(f)是n次代數多項式對f的最佳逼近值，則有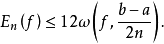

如果f∈C[a,b]有r階連續導數f^(r)∈C[a,b]，那么

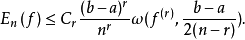這裡C_r是一個僅與r有關的正數。

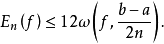
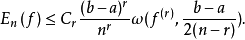
最佳逼近值

記π_n為次數不高於n的代數多項式a₀+a₁x+...+a_nx的全體，這裡a_k(k=0,1,...,n)是實數。對於函式f∈C[a,b]，稱

為n次代數多項式對f在[a,b]上的最佳逼近值（度），也簡稱最佳逼近。