偶校驗英文簡寫EVEN，當實際數據中“1”的個數為偶數的時候，這個校驗位就是“0”，否則這個校驗位就是“1”，這樣就可以保證傳送數據滿足偶校驗的要求。在接收方收到數據時，將按照偶校驗的要求檢測數據中“1”的個數，如果是偶數個“1”，表示傳送正確，否則表示傳送錯誤。
基本介紹
- 中文名：偶校驗
- 外文名：even parity
- 方式：奇校驗和偶校驗
- 定義：偶校驗是數據傳送時採用
- 表示：校驗位就是“1”，否則就是“0”
- 關鍵字：校驗、奇校驗、偶校驗
定義,舉例,行列校驗碼,分布矩陣,生成,校驗,
定義
如果是採用奇校驗，在傳送每一個位元組的時候另外附加一位作為校驗位，當實際數據中“1”的個數為偶數的時候，這個校驗位就是“1”，否則這個校驗位就是“0”，這樣就可以保證傳送數據滿足奇校驗的要求。在接收方收到數據時，將按照奇校驗的要求檢測數據中“1”的個數，如果是奇數，表示傳送正確，否則表示傳送錯誤。
同理偶校驗的過程和奇校驗的過程一樣，只是檢測數據中“1”的個數為偶數,即添加的校驗位使編碼中的1或0的個數為偶數。
舉例
如0100101偶校驗碼就是10100101
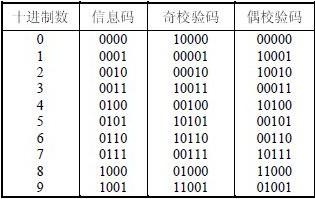
推理偶校驗:當實際數據中“1”的個數為偶數的時候，這個校驗位就是“0”，否則這個校驗位就是“1”，這樣就可以保證傳送數據滿足偶校驗的要求。在接收方收到數據時，將按照偶校驗的要求檢測數據中“1”的個數，如果是偶數個“1”，表示傳送正確，否則表示傳送錯誤。
行列校驗碼
行列校驗碼又稱作水平垂直一致校驗碼或二維奇偶校驗碼，有時還被稱為矩陣碼。它不僅對水平（行）方向的碼元，而且還對垂直（列）方向的碼元實施奇偶校驗。一般L×m個信息元，附加L+m+1個校驗元，由L+1行，m+1列組成一個（Lm+L+m+1，Lm）行列校驗碼的碼字。表8-2就是（66，50）行列校驗碼的一個碼字（L=5，M=10），它的各行和各列對l的數目都實行偶數校驗。可以逐行傳輸，也可以逐列傳輸。解碼時分別檢查各行、各列的校驗關係，判斷是否有錯。
這種碼有可能檢測偶數個錯誤。因為每行的校驗位雖然不能用於檢測本行中的偶數個錯碼，但按列的方向就有可能檢測出來。可是也有一些偶數錯碼不可能檢測出，例如，構成矩形的四個錯碼就檢測不出來。
這種二維奇偶校驗碼適於檢測突發錯碼。因為這種突發錯碼常常成串出現，隨後有較長一段無錯區間，所以在某一行中出現多個奇數或偶數錯碼的機會較多，這種方陣碼適於檢測這類錯碼。前述的一維奇偶校驗碼一般只適於檢測隨機錯誤。
由於方陣碼只對構成矩形四角的錯碼無法檢測，故其檢錯能力較強。一些試驗測量表明，這種碼可使誤碼率降至原誤碼率的百分之一到萬分之一。
二維奇偶校驗碼不僅可用來檢錯，還可用來糾正一些錯碼。例如，當碼組中僅在一行中有奇數個錯誤時，則能夠確定錯碼位置，從而糾正它。
分布矩陣
一個原始的稀疏序列周期移位的位數P是由系統需要的碼率和採用的序列的數目t決定的。由於碼是準循環的，經過列的位置交換以後它的校驗矩陣可以看成是由一些循環子矩陣組合成的。每一個子矩陣能夠通過採樣原校驗矩陣的列得到，採樣周期是p。一個稀疏序列也可以看作是它的p個採樣序列的組合。
如果僅通過交換一個分布矩陣的行或者列就可以得到另一個分布矩陣，我們就說這兩個矩陣是同構的。
生成
當t條好的稀疏序列獲得以後，很容易構造稀疏序列碼的校驗矩陣。首先，把t個稀疏序列作為校驗矩陣的t個關鍵行。其次，通過對關鍵行循環左移，每次移p個位置，不能重複，得到t個子矩陣。最後，把t個子矩陣上下連線就得到了LDPC碼的校驗矩陣。
校驗
國內在JJG1021-1990《產品質量檢驗機構計量認證技術考核規範》及其它一些檔案資料中規定：在沒有檢定規程時，應由企業編寫校驗方法進行校驗。在ISO9001標準的411中，也多處出現"校驗"一詞。如"如果試驗軟體或比較標準用作檢驗手段時，使用前應加以校驗(checked)，……並按規定周期加以復驗(rechecked)。"分析國內外對校驗的用法，其含意基本相同，它與檢定和校準均有一定聯繫又有明顯區別。
它不具有法制性與校準相同，它在技術操作內容上又與檢定有共性，一般可進行校準，也可以對其它有關性能進行規定的檢驗，並最終給出合格性的結論。這一術語有時是很必要的，建議在有關術語定義中應當給校驗一個正式的位置，以統一和規範其使用。
