隨機變數Xij與總平均數的偏差的平方和是刻畫試驗所得全部數據的離散程度的一個指標,因此,各個總體Xi(i=1,2,...,r)是否同分布,可以從偏差平方和中獲得信息,而偏差平方和中包含各總體之間所抽取數據的差異和隨機因素造成的試驗誤差兩部分信息,如果能把偏差平方和中的這兩部分信息分解出來並對其進行比較,就可以達到檢驗假設的目的。
基本介紹
- 中文名:偏差平方和
- 所屬學科:數學
- 所屬問題:數理統計
- 相關問題:單因素試驗及其方差分析
基本介紹
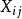
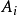




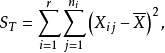
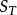
偏差平方和的分解
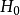
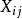

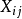
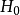



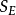
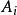
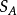
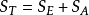
SE與SA的統計特性
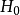
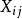




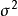


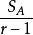
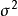
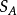
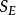


隨機變數Xij與總平均數的偏差的平方和是刻畫試驗所得全部數據的離散程度的一個指標,因此,各個總體Xi(i=1,2,...,r)是否同分布,可以從偏差平方和中獲得信息,而偏差平方和中包含各總體之間所抽取數據的差異和隨機因素造成的試驗誤差兩部分信息,如果能把偏差平方和中的這兩部分信息分解出來並對其進行比較,就可以達到檢驗假設的目的。
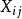
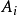




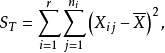
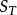
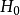
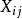

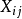
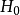



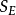
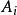
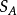
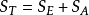
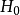
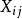




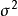


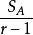
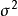
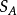
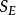

誤差平方和又稱殘差平方和、組內平方和等,根據n個觀察值擬合適當的模型後,餘下未能擬合部份(ei=yi一y平均)稱為殘差,其中y平均表示n個觀察值的平均值,所有n個...
隨機變數Xij與總平均數的偏差的平方和是刻畫試驗所得全部數據的離散程度的一個指標,因此,各個總體Xi(i=1,2,...,r)是否同分布,可以從偏差平方和中獲得信息,...
總平方和(total sum of square),總偏差平方和之簡稱,是指反映全部數據誤差大小的平方和。記為TSS。例如,所抽取的全部23家企業被投訴次數之間的誤差平方和就是總...
效應平方和(sum of squares between groups)又稱“組間離差平方和”,“組間平方和”。它與組內平方和(組內離差平方和)是方差分析中的兩個術語,效應平方和是...
估計誤差平方和,是指通過公式計算出的兩類不確定度平方之和。...... 估計誤差平方和,是指通過公式計算出的兩類不確定度平方之和。估計誤差平方和 Euclidean distan...
組間平方和(sum of squares between groups)是“組間離差平方和(組間偏差平方和)”的簡稱,又稱效應平方和。它與組內平方和(組內離差平方和)是方差分析中的...
中誤差是衡量觀測精度的一種數字標準,亦稱“均方根差”。在相同觀測條件下的一組真誤差平方平均值的平方根。因真誤差不易求得,所以通常用最小二乘法求得的觀測...
定義1:方差分析中組內變異與誤差自由度的商, .定義2:參數估計中均方誤差是指參數估計值與參數真值之差平方的期望值,記為MSE。...
一個量的觀測值或計算值與其真實值之差,特指統計誤差,即一個量在測量、計算或觀察過程中由於某些錯誤或通常由於某些不可控制的因素的影響而造成的變化偏離標準值...
,這部分的值就小,模型不合適,這部分的值就大,稱為失擬誤差,對應的殘差平方和由兩部分構成,一部分是純誤差平方和,另一部分是擬合不佳所引起的擬合誤差平方和。...
1 基本概念 2 EXCEL作誤差線方法 誤差線基本概念 編輯 tips:兩者區別①概念不同;標準差是離均差平方和平均後的方根,標準誤是標準誤差定義為各測量值誤差的平方...
Z的中誤差的平方為mz^2=mx1^2+mx2^2+...+mxn^2n個觀測值代數和(差)的中誤差平方,等於n個觀測值中誤差平方之和。在同精度觀測時,觀測值代數和(差)的...
組間誤差是隨機誤差和系統誤差的總和。例如,四個行業被投訴次數之間的誤差就是組間誤差。數據的誤差用平方和來表示。反映全部數據總誤差大小的平方和稱為總平方和,...
(2) 隨機誤差,如測量誤差造成的差異或個體間的差異,稱為組內差異,用變數在各組的均值與該組內變數值之偏差平方和的總和表示, 記作SSw,組內自由度dfw。...
均方是表示離差平方和與自由度之比。由於各誤差平方和的大小與觀測值的多少有關,為了消除觀測值多少對誤差平方和大小的影響,需要將其平均,也就是用各平方和除以...
然後上在第二步, 找到的每個數據點與樣本平均值之間平方的時差,這些誤差平方進行求和。甚至具有高中單元格 D10,10 的冪在數值示例中不會影響這些誤差平方和在第...
