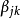信度函式是描述主觀不確定現象的主要數學工具,信度函式與機率函式的主要區別是不滿足可加性,這個性質使它比機率函式能更恰當地表示信息中的“不知性”(ignorance)。
更重要的是,信度函式理論存在Dempster規則,獨立的兩個信度函式可以用此規則合成為一個具有綜合意義的信度函式。
基本介紹
- 中文名:信度函式
- 外文名:belief function
- 提出者:G.Shafter
- 提出時間:1976年
- 基本性質:不滿足可加性
- 是:一種不確定性推理方法
基本概念,定理(mobuis反變換),套用(評價模型),
基本概念
為了方便討論,首先統一下面使用的符號,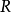 表示實集,
表示實集,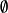 表示空集,
表示空集,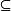 表示包含,
表示包含, 表示集合併,
表示集合併, 表示集合交。集合
表示集合交。集合 的冪集表示為
的冪集表示為 ,對
,對 ,
,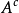 表示
表示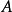 的補集,
的補集,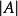 表示集合
表示集合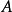 的基,也就是集合
的基,也就是集合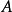 中元素的個數,
中元素的個數, 表示集合
表示集合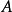 和集合
和集合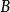 的差集。
的差集。
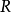
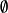
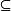





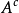
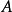
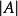
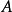
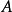

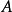
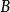
信度函式的一般定義表述為:
假設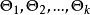 是有限個
是有限個 的劃分,
的劃分,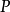 在
在 上的所有概念測度的集合:
上的所有概念測度的集合:
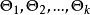

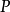


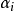
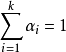
設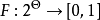 是由下式定義的下界機率:
是由下式定義的下界機率:
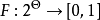

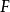
(1)

(2)對 和
和 的
的



在有限集 上信度函式就是一個定義在
上信度函式就是一個定義在 到
到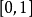 上,且滿足上述兩個條件的集合函式
上,且滿足上述兩個條件的集合函式 。
。


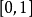

一個隨機集是集值隨機映射。特別的,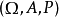 是一個機率空間,
是一個機率空間,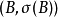 是一個可測空間,其中,
是一個可測空間,其中, 。一個
。一個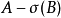 可測映射
可測映射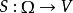 被成為一個隨機集。它的機率法則是在
被成為一個隨機集。它的機率法則是在 上的機率測度
上的機率測度 。事實上,一個在
。事實上,一個在 上的隨機集可以看成是一個在
上的隨機集可以看成是一個在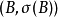 上的機率測度。比如,對有限的
上的機率測度。比如,對有限的 和
和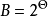 ,
, 就是
就是 的冪集,任一在
的冪集,任一在 上的機率測度(隨機集
上的機率測度(隨機集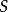 )可以由密度函式
)可以由密度函式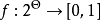 確定。比如,
確定。比如, 並有
並有 。這時,隨機集
。這時,隨機集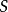 的分布函式
的分布函式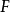 滿足:
滿足:
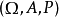
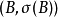

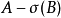
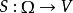



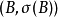

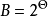



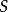
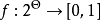


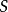
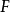
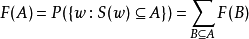

定理(mobuis反變換)
設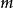 是基本概念指派函式,對任意
是基本概念指派函式,對任意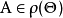 ,有信度函式:
,有信度函式: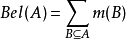 ,則
,則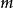 可以被信度函式Bel唯一指定,並有逆轉公式:
可以被信度函式Bel唯一指定,並有逆轉公式:
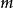
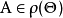
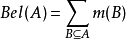
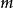

套用(評價模型)
設 是一個評價對象,評價目標分解為
是一個評價對象,評價目標分解為 個指標:
個指標: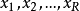 ,對象
,對象 關於
關於 的評價(或標值)記為
的評價(或標值)記為 如果指標
如果指標 仍是比較抽象或綜合的概念,那么可繼續把
仍是比較抽象或綜合的概念,那么可繼續把 作為一個評價對象。設指標
作為一個評價對象。設指標 又分解為
又分解為 個指標
個指標 ,對象
,對象 關於指標
關於指標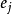 的評價過程
的評價過程 ,於是,對
,於是,對 的評價過程一般形成多層遞階結構。
的評價過程一般形成多層遞階結構。


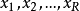









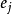


這裡,考慮至少有一個定性屬性的評價問題。一般地,定義評語集合 ,其中
,其中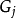 代表屬性標值
代表屬性標值 可能被判定的一個評語。獲得屬性標值
可能被判定的一個評語。獲得屬性標值 的最簡單方式是把它直接評定為某個評語
的最簡單方式是把它直接評定為某個評語 。
。

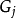



假定評價者給出的因素標值 採用如表1的形式。
採用如表1的形式。


表中, ——因素,
——因素,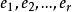 ——關於屬性
——關於屬性 的歸一化相對權重,滿足
的歸一化相對權重,滿足