伽利略螺線

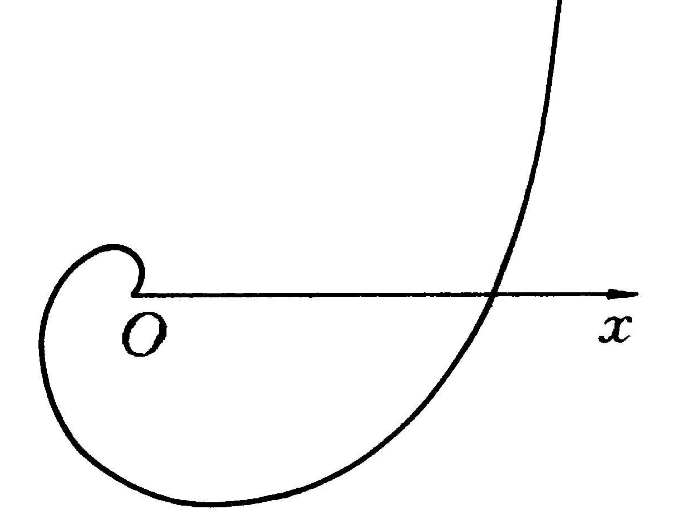
伽利略螺線(Galilei spiral)也稱等加速螺線，是一種特殊曲線。在極坐標系，用ρ=aθ+bθ+c(a、b、c是常數，a≠0)表示的曲線(螺線的一種)稱為伽利略螺線。一個動點沿一條直線作等加速運動，同時這條直線又繞著它上面的一個定點作等角速旋轉時，這個動點的軌跡叫做等加速螺線。

基本介紹

• 中文名：伽利略螺線
• 外文名：Galilei spiral
• 所屬學科：數理科學
• 別名：等加速螺線
• 極坐標方程：ρ=aθ+bθ+c(a≠0)

基本介紹

伽利略螺線亦稱等加速螺線，是一種特殊曲線，極坐標方程為ρ=aθ+bθ+c(a≠0)的曲線稱為伽利略螺線(見圖，b=c=0的情形)，伽利略螺線是17世紀發現的，在地球赤道某地的上方有一個自由落體，當它隨地球一起轉動時，畫出的曲線就是伽利略螺線，它是動點沿著一條定直線作等加速運動，同時這條直線又繞著它上面一點作等角速度旋轉時，動點的軌跡。

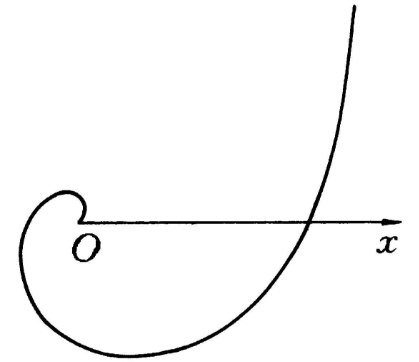
圖1

等加速螺線方程的推導

下面我們推導等加速螺線的方程。

設點O是直線l上一定點，動點M沿直線l作等加速運動，點M在初始位置M₀時的初速為v, q是點M的加速度(q<0為減速度)，同時直線l又以等角速ω繞點O旋轉,求動點M的軌跡的方程。

如圖2,取定點O為極點，直線l的初始位置Ox為極軸建立極坐標系，M₀的極坐標為(ρ₀, 0),動點經過時間t移動到點M。

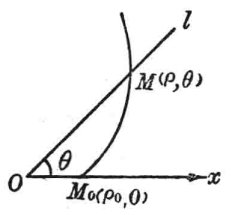
圖2

設動點M的坐標是(ρ, θ),根據等加速螺線的定義有:

消去參數t,得

令得

這是等加速螺線的極坐標方程，其中a、b、c是常數，且a≠0。

等加速螺線的特徵是當直線l作等角速轉動時，動點M沿直線l運動的速度逐漸增加(或減少)。在凸輪的設計中，如果要使從動桿由不動到等速移動，凸輪上對應的輪廓曲線就必須由圓弧變到等速螺線，為了增強機械運動的平穩以及減少凸輪的磨損，在從動桿由不動到等速移動的中間，需要有一個過渡的階段，目的是使從動桿移動的速度從零均勻地增大，直至達到所作等速移動的速度，等加速螺線經常被採用為圓弧到等速螺線之間的過渡曲線。

這時，圓弧的終點就是等加速螺線的起點，因此，從動桿的初速，從而，在這種情況下，等加速螺線的方程具有以下的形式：

這裡a，c是常數，且a≠0。

同樣，等加速螺線也常被採用為等速螺線到圓弧的過渡曲線。

求曲線的極坐標方程的一般步驟如下:

(1) 選擇適當的極坐標系，就是確定極點與極軸的位置;

(2) 用等式表達曲線上任意一點P(ρ，θ)應滿足的條件;

(3) 化簡得出曲線的極坐標方程。

等加速螺線的畫法

我們以為例，畫出它的圖形。

根據方程，列出ρ和θ的對應數值如下表：

把各點連成一條光滑的曲線，就得到等加速螺線的圖形。

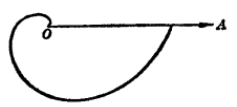
圖3