點P(p1,p2)在曲線F(x,y)=0上運動,由點P的移動,按照一定的關係,引起點M(m1,m2)的移動,則稱點M是點P的伴隨點,M的運動軌跡G(x,y)=0稱為伴隨軌跡.
伴隨拋物線和伴隨直線,伴隨拋物線的性質,例,
伴隨拋物線和伴隨直線
伴隨拋物線(Concomitant parabola)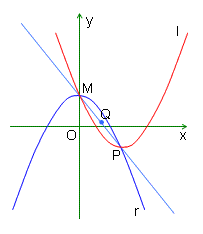

對於拋物線l:y=ax^2+bx+c(其中a,b,c均不為0),它的頂點P的坐標是(-b/(2a),(4ac-b^2)/(4a)),焦參數p=1/(2|a|),與y軸的交點是M(0,c).我們稱以M為頂點,關於y軸對稱,過點P的拋物線r為拋物線l的伴隨拋物線.直線PM為l的伴隨直線.伴隨拋物線r的方程為y=-ax^2+c.伴隨直線PM的方程為y=(b/2)x+c.
伴隨拋物線的性質
伴隨拋物線r的焦參數也是p=1/(2|a|),與原拋物線l形狀相同,大小相等,並且關於線段PM的中點Q中心對稱.Q點的坐標為(-b/(4a),(8ac-b^2)/(8a)).
特別地,拋物線x^2=2py的伴隨拋物線為x^2=-2py,伴隨直線為x軸.
伴隨關係是一種主從關係,不可逆,換言之,一條拋物線的伴隨拋物線的伴隨拋物線不是它本身.
例
(1)寫出拋物線y=2x^2-4x+1的伴隨拋物線和伴隨直線的解析式;
(2)若一條拋物線的伴隨拋物線和伴隨直線方程分別是y=-x^2-3,y=-x-3,求這條拋物線的方程;
(3)若拋物線l:y=ax^2+bx+c與x軸交於A(x1,0)、B(x2,0)兩點,0<x1<x2,它的伴隨拋物線與x軸交於C、D兩點,且AB=CD.求出a,b,c應滿足的條件.
解:
(1)伴隨拋物線的解析式為:y=-2x^2+1 ,伴隨直線的解析式為:y=-2x+1;
(2)所求拋物線的方程為y=x^2-2x-3;
(3)l的伴隨拋物線方程為y=-ax^2+c.設C(x3,0)、D(x4,0),根據韋達定理,x3+x4=0,x3x4=-c/a ,所以|CD|^2=(x4-x3)^2=(x3+x4)^2-4x3x4=4c/a.同理可得,|AB|^2=(x4-x3)^2=(b^2-4ac)/a^2 .因為AB=CD,所以4c/a=(b^2-4ac)/a^2,即b^2-8ac=0,這就是a,b,c應滿足的條件.此時,對稱中心為(-b/(4a),0),在x軸上.
